当前位置：试卷中心 > 试卷详情

2022-2023学年北京八中九年级（上）期中数学试卷

发布：2024/9/24 5:0:8

一、选择题（本题共16分，每小题2分）（每题均有四个选项，符合题意的选项只有一个）

1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
组卷：9引用：1难度：0.8
解析
2．下列方程是一元二次方程的是（　　）
A．x²+y+3=0 B．3x²-2=0 C．
x
2
+
1
x
=
7
D．5x+3=0
组卷：61引用：9难度：0.8
解析
3．已知点A（-1，a），点B（b,2）关于原点对称，则a+b的值是（　　）
A．-1 B．1 C．-2 D．2
组卷：173引用：8难度：0.9
解析
4．一元二次方程x²-5x+2=0的根的情况是（　　）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．无法确定
组卷：327引用：13难度：0.7
解析
5．将二次函数y=x²-2x+3化为y=（x-h）²+k的形式，结果为（　　）
A．y=（x+1）²+4 B．y=（x+1）²+2 C．y=（x-1）²+4 D．y=（x-1）²+2
组卷：4561引用：171难度：0.9
解析
6．已知关于x的一元二次方程（k+1）x²-（2k+1）x+k-1=0有实数根，则k的取值范围是（　　）
A．
k
≥
-
5
4
B．k≠-1
C．
k
＞
-
5
4
且k≠-1 D．
k
≥
-
5
4
且k≠-1
组卷：437引用：7难度：0.6
解析
7．若A（-4，y₁），B（-3，y₂），C（1，y₃）为二次函数y=x²+4x-5的图象上的三点，则y₁，y₂，y₃的大小关系是（　　）
A．y₁＜y₂＜y₃ B．y₂＜y₁＜y₃ C．y₃＜y₁＜y₂ D．y₁＜y₃＜y₂
组卷：1400引用：53难度：0.9
解析
8．四位同学在研究二次函数y=ax²+bx-6（a≠0）时，甲同学发现函数的最小值为-8；乙同学发现当x=2时，y=3；丙同学发现x=3是一元二次方程ax²+bx-6=0（a≠0）的一个根；丁同学发现函数图象的对称轴是直线x=1；已知这四位同学中只有一位同学发现的结论是错误的，则该同学是（　　）
A．甲 B．乙 C．丙 D．丁
组卷：57引用：3难度：0.7
解析

二、填空题（本题共16分，每小题2分）

9．若方程
（
m
-
2
）
x
m
2
-
2
+
3
x
=
0
是关于x的一元二次方程，则m的值为
．
组卷：257引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共68分，17题6分，18-23题每题5分，24-26题每题6分，27、28题每题7分）

27．已知，正方形ABCD，等腰Rt△BEF，其中∠BEF=90°，BE=EF．连接DF，点G为DF的中点，连接EG，CG，EC．

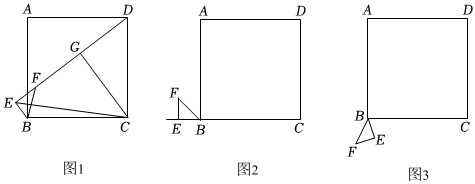
（1）如图1，若BE=1，AB=5，当E，F，D三点共线时，CG=4，则∠GCE=
；
（2）如图2，若点E在CB的延长线上，
①补全图形；
②判断EG与GC的数量和位置关系，并证明；
（3）将图2中的△BEF绕点B逆时针旋转至图3所示位置，在（2）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．
组卷：86引用：2难度：0.1
解析
28．定义：在平面直角坐标系xOy中，点（m,n）是某函数图象上的一点，作该函数图象中自变量大于m的部分关于直线x=m的轴对称图形，与原函数图象中自变量大于或等于m的部分共同构成一个新函数的图象，则这个新函数叫做原函数关于点（m,n）的“派生函数”．
例如：图1是函数y=x+1的图象，则它关于点（0，1）的“派生函数”的图象如图2所示，且它的“派生函数”的解析式为
y
=
x
+
1
（
x
≥
0
）
-
x
+
1
（
x
＜
0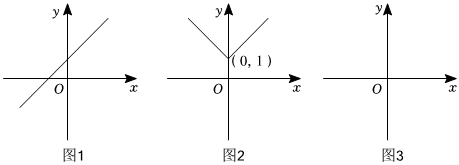
）
．

（1）在图3中画出函数y=x+1关于点（1，2）的“派生函数”的图象；
（2）点M是函数H：y=-x²+6x-8的图象上的一点，设点M的横坐标为m,H'是函数H关于点M的“派生函数”．
①当m=1时，若函数值y'的范围是-3≤y'≤1，求此时自变量x的取值范围；
②直接写出以点A（2，2），B（-2，2），C（-2，-2），D（2，-2）为顶点的正方形ABCD与函数H'的图象只有两个公共点时，m的取值范围．
组卷：410引用：3难度：0.3
解析