当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市部分区高一（下）期末数学试卷

发布：2024/5/30 8:0:9

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．复数z=1-i的虚部是（　　）
A．1 B．-1 C．i D．-i
组卷：172引用：14难度：0.9
解析
2．已知点C在线段AB上，且AC=2CB，若向量
AC
=
λ
AB
，则λ=（　　）
A．2 B．
1
2
C．
3
2
D．
2
3
组卷：33引用：3难度：0.7
解析
3．某校高中生共有3000人，其中高一年级900人，高二年级600人，高三年级1500人，现采用分层抽样的方法随机抽取容量为150人的样本，那么高一、高二、高三年级被抽取的人数分别为（　　）
A．45，30，75 B．45，15，90 C．30，30，90 D．60，30，60
组卷：31引用：2难度：0.7
解析
4．若向量
a
=（4，2），
b
=（6，k），若
a
∥
b
，则k=（　　）
A．-12 B．12 C．-3 D．3
组卷：401引用：8难度：0.8
解析
5．函数
f
（
x
）
=
2
sin
（
x
+
π
3
）
，x∈[0，π]的单调递减区间是（　　）
A．
[
0
，
π
6
]
B．
[
0
，
5
π
6
]
C．[0，π] D．
[
π
6
，
π
]
组卷：484引用：5难度：0.7
解析
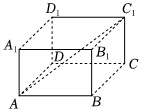6．如图，在长方体ABCD-A₁B₁C₁D₁中，AB=2，BC=CC₁=1．则直线AC₁与平面BB₁C₁C所成角的余弦值是（　　）
A．
3
2
B．
1
2
C．
3
3
D．
1
3
组卷：173引用：3难度：0.7
解析
7．2023年4月10日，重庆市中学生田径锦标赛在奉节举行．本次锦标赛设有长跑、短跑、跳高、跳远、铅球等项目，某参赛队员要从短跑、跳高、跳远、铅球4个项目中任选2项，假设每个项目被选中的可能性相等，那么跳高和铅球至少有一门被选中的概率是（　　）
A．
1
6
B．
1
2
C．
2
3
D．
5
6
组卷：26引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共有6个小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.

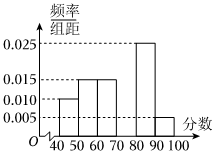21．“杭州2022年第19届亚运会”将于2023年9月23日至10月8日在中国浙江杭州举行．在杭州亚运会倒计时两周年之际，由杭州亚运会组委会与中国日报社联合主办的“杭州2022年第19届亚运会”双语学生记者活动正式启动．为助力杭州亚运会宣传工作，向世界讲好中国故事，奏响亚运最强音．杭州市相关部门积极组织学生报名参加选拔考试，现从参加考试的学生中抽出60名，将其成绩（成绩均为整数）分成[40，50），[50，60），……，[90，100]六组，并画出如图所示的部分频率分布直方图，观察图形，回答下列问题：
（1）求第四组的频率，并补全这个频率分布直方图；
（2）请根据频率分布直方图，估计样本的中位数和方差．（每组数据以区间的中点值为代表）．
组卷：46引用：2难度：0.7
解析
22．已知向量
m
=
（
cosωx
-
sinωx
,
2
sinωx
）
，
n
=
（
cosωx
+
sinωx
,
3
cosωx
）
（
ω
＞
0
）
，函数
f
（
x
）
=
m
•
n
+
t
，若f（x）图象上一个最高点和它相邻最低点之间的水平距离为
π
2
，图象过点
（
π
6
，
1
）
．
（1）求f（x）表达式和f（x）的单调减区间；
（2）将函数f（x）的图象向右平移
π
4
个单位，再将图象上各点的横坐标伸长到原来的4倍（纵坐标不变），得到函数y=g（x）的图象，若函数F（x）=g（x）-k在区间[0，2π]上有且只有一个零点，求实数k的取值范围；
（3）若函数h（x）=x²-2mx+1，在（2）的条件下，若当x₁∈[0，2]时，总有
x
2
∈
[
π
3
，
5
π
3
]
使得h（x₁）=g（x₂），求实数m的取值范围．
组卷：43引用：1难度：0.5
解析