2021-2022学年江苏省宿迁市泗洪县八年级（上）期中数学试卷
发布：2024/9/28 18:0:2
一、选择题（本题共8小题，每小题3分，共24分）
-
1．第24届冬奥会将于2022年在北京和张家口举办，中国将是第一个实现奥运“全满贯”（先后举办奥运会、残奥会、青奥会、冬奥会、冬残奥会）的国家．下列四个图分别是冬奥会图标中的一部分，其中是轴对称图形的为（ ）
组卷：7引用：1难度：0.9 -
2．一个等腰三角形的底角是40°，则它的顶角是（ ）
组卷：297引用：5难度：0.9 -
3．下列说法正确的是（ ）
组卷：2230引用：78难度：0.9 -
4．已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件中不能判断△ABC是直角三角形的是（ ）
组卷：508引用：9难度：0.5 -
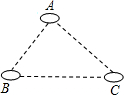5．如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）组卷：2299引用：122难度：0.9 -
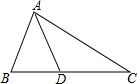6．如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为（ ）组卷：9619引用：130难度：0.9 -
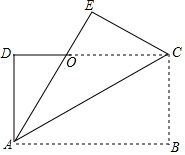7．如图，在长方形纸片ABCD中，AD=4cm,把纸片沿直线AC折叠，点B落在E处，AE交DC于点O，若OC=5cm,则CD的长为（ ）组卷：427引用：3难度：0.7 -
8．《九章算术》是古代东方数学代表作，书中记载：今有开门去阃（读kǔn,门槛的意思）一尺，不合二寸，问门广几何？题目大意是：如图1、2（图2为图1的平面示意图），推开双门，双门间隙CD的距离为2寸，点C和点D距离门槛AB都为1尺（1尺=10寸），则AB的长是（ ）
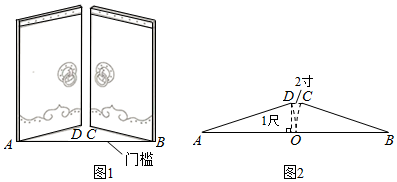组卷：4873引用：56难度：0.5
二、填空题（本题共10小题，每小题3分，共30分）
-
9．一个等边三角形的对称轴有条．
组卷：553引用：31难度：0.9
五、解答题（本大题共2题，每题12分，共24分）
-
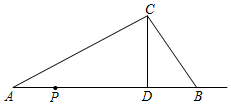27．如图，△ABC中，CD为AB边上的高，AD=8，CD=4，BD=3．动点P从点A出发，沿射线AB运动，速度为1个单位/秒，运动时间为t秒．
（1）当t为何值时，△PDC≌△BDC；
（2）当t为何值时，△PBC是等腰三角形？组卷：239引用：4难度：0.6 -
28．【问题提出】
学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．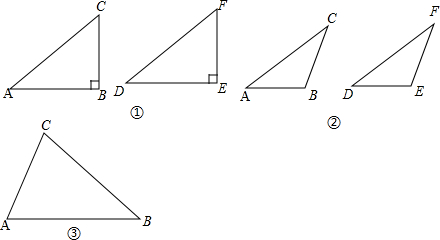
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．组卷：283引用：13难度：0.3
