2023年宁夏银川市兴庆区唐徕中学中考数学三模试卷
发布：2024/6/20 8:0:9
一、选择题（本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中只有一项是符合题目
-
1．按照我国《生活垃圾管理条例》要求，到2025年底，我国地级及以上城市要基本建成垃圾分类处理系统，下列垃圾分类指引标志图形中，是轴对称图形又是中心对称图形的是（ ）
组卷：196引用：6难度：0.9 -
2．x=1是关于x的一元二次方程x2+ax+2b=0的解，则4a+8b=（ ）
组卷：514引用：6难度：0.7 -
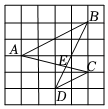3．如图，在边长为1的小正方形组成的网格中，A，B，C，D四个点均在格点上，AC与BD相交于点E，连接AB，CD，则△ABE与△CDE的周长比为（ ）组卷：2291引用：19难度：0.4 -
4．实数a在数轴上的对应位置如图所示，则+1+|a-1|的化简结果是（ ）a2组卷：2165引用：20难度：0.6 -
5．为了解“睡眠管理”落实情况，某初中学校随机调查50名学生每天平均睡眠时间（时间均保留整数），将样本数据绘制成统计图（如图），其中有两个数据被遮盖．关于睡眠时间的统计量中，与被遮盖的数据无关的是（ ）组卷：1078引用：21难度：0.7 -
6．已知二次函数y=x2-2x-3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3．当-1＜x1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（ ）
组卷：5706引用：30难度：0.5 -
7．在同一平面直角坐标系中，函数y=ax+b与
（其中a,b是常数，ab≠0）的大致图象是（ ）y=bax组卷：3197引用：16难度：0.6 -
8．如图，在平面直角坐标系中，点A在y轴的正半轴上，OA=1，将OA绕点O顺时针旋转 45° 到 OA1，扫过的面积记为 S1，A1A2⊥OA1 交x轴于点A2；将 OA2 绕点O顺时针旋转 45°到 OA3，扫过的面积记为S2，A3A4⊥OA3 交y轴于点A4；将 OA4 绕点O顺时针旋转 45°到 OA5扫过的面积记为 S3；…；按此规律，则 S2023 为（ ）组卷：123引用：2难度：0.5
三、解答题（本大题共10小题，共72分.解答应写出必要的文字说明、证明过程或演算步骤）
-
25．第二十四届冬奥会在北京成功举办，我国选手在跳台滑雪项目中夺得金牌．在该项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．本项目主要考核运动员的飞行距离和动作姿态．某数学兴趣小组对该项目中的数学问题进行了深入研究：如图为该兴趣小组绘制的赛道截面图，以停止区CD所在水平线为x轴，过起跳点A与x轴垂直的直线为y轴，O为坐标原点，建立平面直角坐标系．着陆坡AC的坡角为 30°，OA=60m.某运动员在A处起跳腾空后，飞行至着陆坡的B处着陆，AB=100m.在空中飞行过程中，运动员到x轴的距离y（m）与水平方向移动的距离x（m）具备二次函数关系，其解析式为
．y=-150x2+bx+c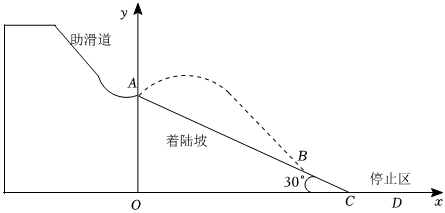
（1）求b,c的值
（2）进一步研究发现，该运动员在飞行过程中，其水平方向移动的距离x（m）与飞行时间t（s）具备一次
函数关系：x=kt+m,当运动员在起跳点腾空时，t=0，x=0；空中飞行5s后着陆．
①求x关于t的函数解析式；
②当t为何值时，运动员离着陆坡的竖直距离h（m）最大，最大值是多少？组卷：165引用：1难度：0.5 -
26．综合与实践
问题情景：在Rt△ABC中，∠BAC=90°，AB=3，AC=4．直角三角板EDF中，∠EDF=90°，将三角板的直角顶点D放在Rt△ABC斜边BC的中点处，并将三角板绕点D旋转，三角板的两边DE，DF分别与边AB，AC交于点M，N．
猜想证明：
（1）如图①，在三角板旋转过程中，当M为边AB的中点时，试判断四边形AMDN的形状，并说明理由；
问题解决：
（2）如图②，在三角板旋转过程中，当∠C=∠1时，求线段CN的长；
（3）如图③，在三角板旋转过程中，当∠B=∠2时，请直接写出线段CN的长为 ．组卷：70引用：3难度：0.3
