2022-2023学年浙江省宁波市慈溪市科学中学八年级（上）期中数学试卷

一、选择题（每题3分，共30分，在每小题给出的四个选项中，只有一项符合题目要求）

• 1．下列选项是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（　　）

  A． 打喷嚏捂鼻子	B． 喷嚏后慎揉眼
  C． 戴口罩讲卫生	D． 勤洗手勤通风
  组卷：39引用：5难度：0.8

  解析

• 2．在平面直角坐标系中，与点P关于原点对称的点Q为（1，-3），则点P的坐标是（　　）

  A．（1，3）

  B．（-1，-3）

  C．（1，-3）

  D．（-1，3）
  组卷：230引用：8难度：0.7

  解析

• 3．不等式组

  x - 5 ≤ 0

  x + 1 ＞ 0

  的解集在数轴上表示为（　　）

  A．

  B．

  C．

  D．
  组卷：215引用：7难度：0.6

  解析

• 4．等腰三角形的一个角是70°，则它顶角的度数是（　　）

  A．70°

  B．40°

  C．70°或20°

  D．70°或40°
  组卷：213引用：3难度：0.6

  解析

• 5．若y=（m+4）x+m-4是正比例函数，则点（2+m,2-m）所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：106引用：2难度：0.8

  解析

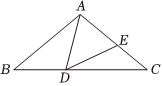• 6．如图，在△ABC中，AB=AC，点D在BC上，点E在AC上，且DA=DE，若∠BAD=35°，∠EDC=25°，则∠DAE的度数为（　　）

  A．80°

  B．65°

  C．60°

  D．50°
  组卷：458引用：4难度：0.7

  解析

• 7．某商贩分两次买苹果，第一次买了30斤，价格为每斤x元，第二次买了20斤，价格为每斤y元．后来他以每斤

  x

  +

  y

  2

  元的价格卖完，结果发现自己赔了钱，下面判断x与y的大小关系正确的是（　　）

  A．x≥y

  B．x≤y

  C．x＞y

  D．x＜y
  组卷：140引用：3难度：0.7

  解析

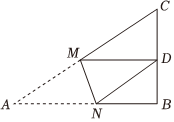• 8．如图，Rt△ABC中，AB=4，BC=3，∠B=90°，M，N分别是边AC，AB上的两个动点，将△ABC沿直线MN折叠，使得点A的对应点D落在BC边的中点处，则线段BN的长为（　　）

  A． 55 32

  B． 73 32

  C． 5 6

  D． 13 6
  组卷：99引用：3难度：0.5

  解析

三、解答题（第17、18题各6分，第19题7分，第20、21题各8分，第22题9分，第23题10分，第24题12分，共66分）

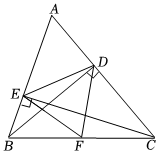• 23．在△ABC中，CE，BD是高，F是BC的中点．
  （1）求证：△EFD是等腰三角形；
  （2）∠A=45°，求∠EFD度数；
  （3）BC=4，S_△EFD=1，求∠A．
  组卷：130引用：2难度：0.7

  解析

• 24．已知：△ABC中，∠ACB=90°，AC=CB，D为直线BC上一动点，连接AD，在直线AC右侧作AE⊥AD，且AE=AD．
  
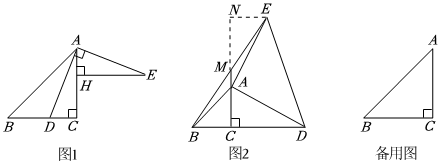
  （1）如图1，当点D在线段BC上时，过点E作EH⊥AC于H，连接DE．求证：EH=BC；
  （2）如图2，当点D在线段BC的延长线上时，连接BE交CA的延长线于点M，求证：BM=EM；
  （3）当点D在直线CB上时，连接BE交直线AC于M，若2AC=7CM，请求出

  S

  △

  ADB

  S

  △

  AEM

  的值．
  组卷：302引用：3难度：0.5

  解析