2022-2023学年福建省厦门一中高三(上)月考数学试卷(12月份)
发布:2024/7/24 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x|log2x≥1},B={x|x2-x-6<0},则(∁RA)∩B等于( )
组卷:66引用:7难度:0.9 -
2.已知函数f(x)=
,则f(f(4))的值为( )log12x,x>03x,x≤0组卷:149引用:12难度:0.9 -
3.现行普通高中学生在高一时面临着选科的问题,某学校抽取了部分男、女同学选科意愿的一份样本,制作出如图两个等高堆积条形图.根据这两幅图中的信息,下列哪个统计结论是不正确的( )
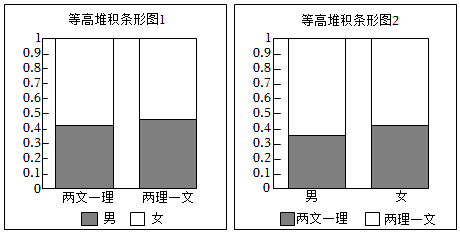 组卷:152引用:3难度:0.8
组卷:152引用:3难度:0.8 -
 4.如图,ABCD是边长为的正方形,点E,F分别是边BC,CD的中点,将△ABE,△CEF,△ADF分别沿AE,EF,FA折起,使得B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球的球面上,则该球的表面积是( )23组卷:57引用:3难度:0.7
4.如图,ABCD是边长为的正方形,点E,F分别是边BC,CD的中点,将△ABE,△CEF,△ADF分别沿AE,EF,FA折起,使得B,C,D三点重合于点P,若四面体PAEF的四个顶点在同一个球的球面上,则该球的表面积是( )23组卷:57引用:3难度:0.7 -
5.已知f(x)=
+ax+cos2x,若f(2x2x+1)=2,则f(-π3)等于( )π3组卷:23引用:2难度:0.9 -
6.数列{an}满足a1=
,a2=28,(an>0),3333=an2-an-12an-12(n≥2),则a2017=( )an+12-an2an+12组卷:180引用:6难度:0.7 -
7.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,分别过A、B两点作准线的垂线,垂足分别为A′、B′两点,以线段A′B′为直径的圆C过点(-2,3),则圆C的方程为( )
组卷:302引用:7难度:0.5
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知椭圆E:
+x2a2=1(a>b>0)的左、右焦点分别为F1,F2,离心率为y2b2,过点F1的直线l,交椭圆E于A、B两点,过点F2的直线l2交椭圆E于C,D两点,且AB⊥CD,当CD⊥x轴时,|CD|=3.12
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)求四边形ACBD面积的最小值.组卷:59引用:3难度:0.5 -
22.已知函数
.f(x)=exlnx-1,g(x)=xex
(1)若g(x)=a在(0,2)上有两个不等实根,求实数a的取值范围;
(2)证明:>0.f(x)+2eg(x)组卷:101引用:2难度:0.1


