2023-2024学年山东省青岛五十八中高三(上)期初数学试卷
发布:2024/7/20 8:0:8
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x∈N|x≤5},集合B={x|x(x-2)>0},则A∩B=( )
组卷:423引用:9难度:0.8 -
2.已知复数z满足z(1-i)=3-i,则
=( )z•z组卷:112引用:7难度:0.7 -
3.已知一组样本数据(x1,y1),(x2,y2),…,(xn,yn),根据这组数据的散点图分析x与y之间的线性相关关系,若求得其线性回归方程为
=-30.4+13.5x,则在样本点(9,53)处的残差为( )̂y组卷:262引用:6难度:0.8 -
4.某调查机构抽取了部分关注济南地铁建设的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图.根据图中(35岁以上含35岁)的信息,关于该样本的结论不一定正确的是( )
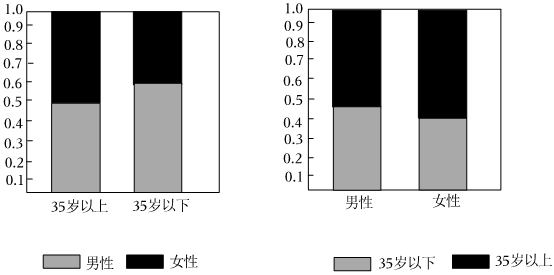 组卷:111引用:4难度:0.7
组卷:111引用:4难度:0.7 -
5.已知函数
的最小正周期为T.若f(x)=4cos(2x+φ)(|φ|<π2),则f(T8)=2-6=( )f(-π4)组卷:35引用:3难度:0.7 -
6.已知底面半径为3的圆锥SO,其轴截面为正三角形,若它的一个内接圆柱的底面半径为1,则此圆柱的侧面积为( )
组卷:56引用:2难度:0.7 -
7.田忌赛马是中国古代对策论与运筹思想的著名范例.故事中齐将田忌与齐王赛马,孙膑献策以下马对齐王上马,以上马对齐王中马,以中马对齐王下马,结果田忌一负两胜从而获胜.该故事中以局部的牺牲换取全局的胜利成为军事上一条重要的用兵规律,在比大小游戏中(大者为胜),已知我方的三个数为a=cosθ,b=sinθ+cosθ,c=cosθ-sinθ,对方的三个数以及排序如表:
当0<θ<第一局 第二局 第三局 对方 2tanθ sinθ 时,则我方必胜的排序是( )π4组卷:165引用:12难度:0.8
四、解答题:本大题共6小题,共70分.
-
21.已知椭圆C:
经过点x2a2+y2b2=1(a>b>0),且与椭圆(-23,3)有共同的焦点.x27+y23=1
(1)求椭圆C的标准方程;
(2)设直线l与椭圆C交于A,B两点,与y轴交于点P,O为坐标原点.若,求点P的坐标.OA•PB+OB•PA=-24组卷:68引用:5难度:0.5 -
22.已知函数
,a∈R.f(x)=(1+1x)lnx+a+1x
(1)若f(x)在(0,+∞)上是增函数,求a的取值范围;
(2)若f(x)在[1,e]上的最小值h(a)>3a+3,求a的取值范围.组卷:29引用:4难度:0.3


