2023-2024学年江西省南昌二十八中教育联盟九年级(上)期中数学试卷
发布:2024/10/3 3:0:2
一、单选题(本大题共6小题,每小题3分,共计18分)
-
1.第19届杭州亚运会因疫情推迟到2023年,如图所示有关的图案中,中心对称图形是( )
组卷:19引用:2难度:0.9 -
2.已知一元二次方程3x2-5x-1=0的二次项系数为3,则一次项系数为( )
组卷:101引用:7难度:0.8 -
 3.如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )组卷:293引用:4难度:0.5
3.如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )组卷:293引用:4难度:0.5 -
4.若关于x的方程mx2-4x+3=0有实数根,则m的取值范围是( )
组卷:951引用:4难度:0.5 -
5.对于y=2(x-3)2-4的图象,下列叙述错误的是( )
组卷:248引用:4难度:0.6 -
6.在同一平面直角坐标系中,函数y=mx+m和函数y=-mx2+2x+2(m是常数,且m≠0)的图象可能是( )
组卷:2630引用:47难度:0.7
二、填空题(本大题共6小题,每小题3分,共计18分)
-
7.已知M(a,-3)和N(4,b)关于原点对称,则a+b= .
组卷:554引用:14难度:0.8
五、解答题(本大题共2小题,每小题9分,共计18分)
-
22.通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,试猜想EF、BE、DF之间的数量关系.
(1)思路梳理:把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,由∠ADG=∠B=90°,得,∠FDG=180°,即点F、D、G共线,易证△AFG≌,故EF、BE、DF之间的数量关系为 .
(2)类比引申:如图2,点E、F分别在正方形ABCD的边CB、DC的延长线上,∠EAF=45°.连接EF,试猜想EF、BE、DF之间的数量关系为 ,并给出证明.
(3)联想拓展:如图3,在△ABC中,已知∠BAC=45°,AD⊥BC垂足于点D,且BD=6,CD=4.求AD的长.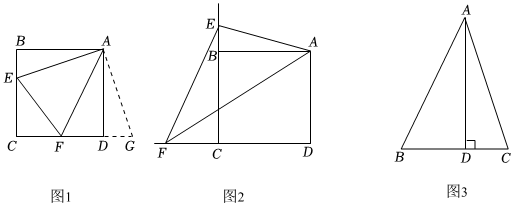 组卷:175引用:2难度:0.1
组卷:175引用:2难度:0.1
六、解答题(本大题共1小题,每小题12分,共计12分)
-
23.如图,抛物线y=
x2-2x-6与x轴相交于点A、点B,与y轴相交于点C.12
(1)请直接写出点A,B,C的坐标;
(2)若点P是抛物线BC段上的一点,当△PBC的面积最大时求出点P的坐标,并求出△PBC面积的最大值;
(3)点F是抛物线上的动点,作FE∥AC交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.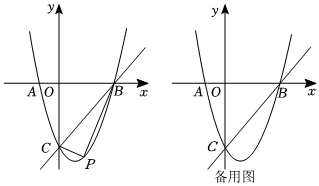 组卷:615引用:5难度:0.1
组卷:615引用:5难度:0.1


