2022-2023学年内蒙古鄂尔多斯市康巴什实验中学九年级（上）第一次月考数学试卷
发布：2024/8/20 5:0:1
一、选择题（10小题，每小题3分，共30分）
-
1．下列是四届冬奥会会徽的部分图案，其中既是轴对称图形，又是中心对称图形的是（ ）
组卷：119引用：5难度：0.9 -
2．如果2是方程x2-3x+c=0的一个根，那么c的值是（ ）
组卷：160引用：16难度：0.9 -
3．对于二次函数y=（x-1）2+2的图象，下列说法正确的是（ ）
组卷：581引用：8难度：0.9 -
4．参加一次聚会的每两人都握了一次手，所有人共握手10次，若共有x人参加聚会，则根据题意，可列方程（ ）
组卷：491引用：8难度：0.8 -
5．将抛物线y=x2向左平移2个单位，再向下平移5个单位，平移后所得新抛物线的表达式为（ ）
组卷：3630引用：28难度：0.7 -
6．二次函数y=ax2+bx+2（a≠0）的图象经过点（-1，1），则代数式1-a+b的值为（ ）
组卷：342引用：7难度：0.7 -
7．二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是（ ）
组卷：9715引用：49难度：0.6 -
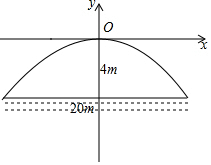8．有一座抛物线形拱桥，正常水位桥下面宽度为20米，拱顶距离水平面4米，如图建立直角坐标系，若正常水位时，桥下水深6米，为保证过往船只顺利航行，桥下水面宽度不得小于18米，则当水深超过多少米时，就会影响过往船只的顺利航行（ ）组卷：1203引用：3难度：0.5
三.简答题（8小题，共72分.解答题应写出文字说明，证明过程或演算步骤）
-
23．如图1，抛物线y=ax2+bx-4a经过A（-1，0），C（0，4）两点，与x轴交于另一点B．
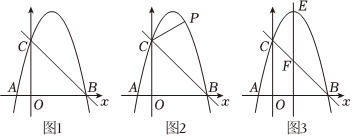
（1）求抛物线和直线BC的解析式；
（2）如图2，点P为第一象限抛物线上一点，是否存在使四边形PBOC面积最大的点P？若存在，求出点P的坐标；若不存在，请说明理由；
（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与直线BC相交于点F，M为直线BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，请求出点N的坐标；若不能，请说明理由．组卷：42引用：2难度：0.1 -
24．问题提出
（1）如图1，在Rt△ABC中，CA=CB，∠ACB=90°，P为此三角形内的一点，且PB=1，PC=2，PA=3，将△CPB绕点C沿顺时针方向旋转90°至△CQA，则∠BPC的度数为 ．
问题探究
（2）如图2，在四边形ACBD中，∠ACB=∠ADB=90°，AC=BC，探究线段AD、BD、CD之间的数量关系并写出解答过程．
问题解决
（3）如图3是某公园内“少儿活动中心”的设计示意图，已知四边形ACBD中，∠ACB=∠ADB=90°，AC=BC，AB=70m,DC平分∠ADB交AB于点P，PE⊥AD于点E，PF⊥BD于点F．按设计要求，四边形PEDF内部为室内活动区，阴影部分是户外活动区，若AP的长为30m,则阴影部分的面积为 m2．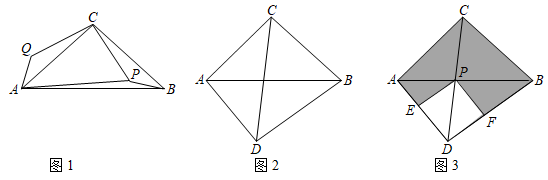
组卷：571引用：6难度：0.3
