当前位置：试卷中心 > 试卷详情

2023-2024学年广西大学附中九年级（上）第二次月考数学试卷

发布：2024/9/17 13:0:8

一、选择题（共10小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑.）

1．下列图形中，不是中心对称图形的是（　　）
A． B． C． D．
组卷：501引用：10难度：0.9
解析
2．点P（2，-3）关于原点对称的点P′的坐标是（　　）
A．（2，3） B．（-2，-3） C．（-3，2） D．（-2，3）
组卷：1040引用：8难度：0.9
解析
3．如图是“光盘行动”的宣传海报（部分），图中餐盘与筷子可看成直线和圆的位置关系是（　　）
A．相切 B．相交 C．相离 D．平行
组卷：445引用：12难度：0.7
解析
4．掷两枚质地均匀的骰子，下列事件是随机事件的是（　　）
A．点数的和为1 B．点数的和为6
C．点数的和大于12 D．点数的和小于13
组卷：1506引用：24难度：0.7
解析
5．已知点P到圆心O的距离为5，若点P在圆内，则⊙O的半径可能为（　　）
A．3 B．4 C．5 D．6
组卷：1481引用：26难度：0.5
解析
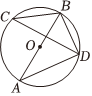6．如图，AB是⊙O的直径，∠BCD=40°，则∠ABD 的大小为（　　）
A．60° B．50° C．45° D．40°
组卷：652引用：7难度：0.6
解析
7．已知点A（-1，y₁），B（6，y₂）是抛物线y=（x-2）²-k上的两点，则y₁，y₂的大小关系为（　　）
A．y₁＜y₂ B．y₁＞y₂ C．y₁=y₂ D．无法确定
组卷：503引用：5难度：0.7
解析
8．在一次聚会上，每两个人之间都互相赠送了一份礼物，若一共送出了90份礼物，则参加聚会的人有（　　）
A．9人 B．10人 C．11人 D．12人
组卷：2206引用：14难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共72分.

25．阅读材料，解答问题：
已知实数m,n满足m²-m-1=0，n²-n-1=0，且m≠n,则m,n是方程x²-x-1=0的两个不相等的实数根，由根与系数的关系可知m+n=1，mn=-1．
根据上述材料，解决以下问题：
（1）直接应用：已知实数a,b满足：a²-7a+1=0，b²-7b+1=0且a≠b,则a+b=
，ab=
；
（2）间接应用：在（1）条件下，求
b
a
+
a
b
的值；
（3）拓展应用：已知实数m,n满足：
1
m
2
+
1
m
=
7
，n²-n=7且mn+1≠0，求
1
m
-
n
的值．
组卷：250引用：4难度：0.5
解析
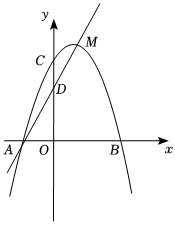26．如图，抛物线y=-x²+bx+c经过A（-1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．
（1）求该抛物线的表达式；
（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；
（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．
组卷：6114引用：17难度：0.3
解析