2022-2023学年四川省达州市万源四中八年级（下）期末数学试卷
发布：2024/7/14 8:0:9
一、选择题（每小题4分，共40分）
-
1．下列图标中，既是轴对称图形，又是中心对称图形的是（ ）
组卷：94引用：2难度：0.9 -
2．不等式（1-a） x＞2变形后得到
成立，则a的取值（ ）x＜21-a组卷：202引用：2难度：0.7 -
3．下列等式从左到右的变形，属于因式分解的是（ ）
组卷：1159引用：160难度：0.9 -
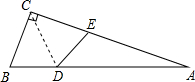4．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（ ）组卷：1380引用：92难度：0.9 -
5．下列分式的值，可以为零的是（ ）
组卷：901引用：5难度：0.9 -
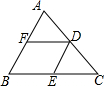6．如图，在△ABC中，AB=4，BC=6，DE、DF是△ABC的中位线，则四边形BEDF的周长是（ ）组卷：1447引用：9难度：0.7 -
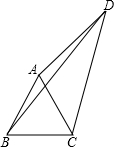7．如图，四边形ABCD中，AC，BD是对角线，△ABC是等边三角形．∠ADC=30°，AD=3，BD=5，则CD的长为（ ）组卷：3316引用：18难度：0.7 -
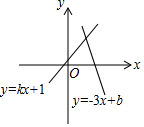8．一次函数y=-3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式kx+1≥-3x+b的解集在数轴上表示正确的是（ ）组卷：2919引用：13难度：0.9
三、解答题（共10小题，共90分）
-
24．在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．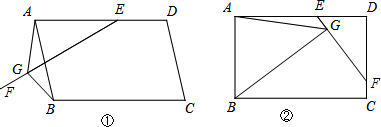
组卷：5548引用：10难度：0.1 -
25．阅读与理解：
图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（点C与点C′重合）的图形．
操作与证明：
（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2，在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α（0°≤α≤360°），连接AD，BE，如图3，在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；
猜想与发现：
根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大，最大是多少？当α为多少度时，线段AD的长度最小，最小是多少？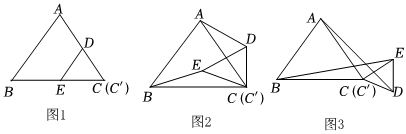
组卷：90引用：9难度：0.1
