2022-2023学年吉林省长春五中高一（下）期末数学试卷

一．单选题（本题共8小题，每小题4分，共32分）

• 1．若z（1-i）=1-5i,则

  z

  =（　　）

  A．-2-2i

  B．-2+2i

  C．3-2i

  D．3+2i
  组卷：45引用：2难度：0.8

  解析

• 2．已知向量

  a

  =（2，3），

  b

  =（-1，2），若m

  a

  +

  b

  与

  a

  -2

  b

  共线，则m的值为（　　）

  A．-2

  B．2

  C． 1 2

  D． - 1 2
  组卷：211引用：4难度：0.9

  解析

• 3．已知m,n,l是三条不同的直线，α，β，γ是三个不重合的平面，则下列说法正确的是（　　）

  A．α⊥γ，β⊥γ，α∩β=l,则l⊥γ

  B．m与n异面，l⊥m,l⊥n,则不存在α，使得l⊥α，m∥α，n∥α

  C．m∥α，n∥β，α⊥β，则m⊥n

  D．m⊥α，m⊥β，n⊥α，则n∥β
  组卷：80引用：3难度：0.7

  解析

• 4．已知动点Q在△ABC所在平面内运动，若对于空间中任意一点P，都有

  PQ

  =

  -

  2

  PA

  +

  5

  PB

  +

  m

  CP

  ，则实数m的值为（　　）

  A．0

  B．2

  C．-1

  D．-2
  组卷：199引用：9难度：0.8

  解析

• 5．下列命题中是真命题的有（　　）

  A．一组数据2，1，4，3，5，3的平均数、众数、中位数相同

  B．有A、B、C三种个体按3：1：2的比例分层抽样调查，如果抽取的A个体数为9，则样本容量为30

  C．若甲组数据的方差为5，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是甲

  D．一组数1，2，2，2，3，3，3，4，5，6的80%分位数为4
  组卷：236引用：7难度：0.9

  解析

• 6．正三棱台ABC-A₁B₁C₁中，AA₁⊥平面B₁BCC₁，AB=2A₁B₁，则异面直线AB₁与BC₁所成角的余弦值为（　　）

  A． 2 5

  B． 3 5

  C． 4 5

  D． 21 5
  组卷：154引用：4难度：0.4

  解析

• 7．在正方体ABCD-A₁B₁C₁D₁中，点P满足

  AP

  =λ

  AB

  +

  1

  3

  A

  A

  1

  （λ∈[0，1]），若平面BDP∥平面B₁CD₁，则实数λ的值为（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  组卷：282引用：6难度：0.6

  解析

四．解答题（本题共5个大题，共56分。解答应写出文字说明、证题过程或演算步骤）

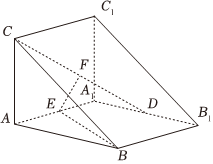• 20．直三棱柱ABC-A₁B₁C₁中，AA₁=AB=AC=2，AA₁⊥AB，AC⊥AB，D为A₁B₁的中点，E为AA₁的中点，F为CD的中点．
  （1）求证：EF∥平面ABC；
   （2）求平面A₁CD与平面CC₁D所成二面角的余弦值．
  组卷：82引用：1难度：0.6

  解析

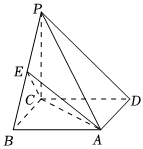• 21．如图，在四棱锥P-ABCD中，已知底面ABCD是正方形，PC⊥底面ABCD，且PC=BC=1，E是棱PB上一点．
  （1）若PD∥平面ACE，证明：E是PB的中点；
  （2）线段PB上是否存在点E，使二面角P-AC-E的余弦值是

  6

  3

  ？若存在，求

  PE

  BE

  的值；若不存在，请说明理由．
  组卷：38引用：6难度：0.4

  解析