2023-2024学年江苏省南京第二十七高级中学高二（上）期初数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知i为虚数单位，若复数

  z

  =

  1

  -

  3

  i

  1

  -

  i

  ，则z的虚部为（　　）

  A．-i

  B．-1

  C．0

  D．1
  组卷：20引用：2难度：0.8

  解析

• 2．若直线x+ay-2=0与直线ax+y-a-1=0平行，则a的值为（　　）

  A．1

  B．1或-1

  C．-1

  D．0
  组卷：114引用：2难度：0.5

  解析

• 3．在长方体ABCD-A₁B₁C₁D₁中，已知点P为线段D₁C₁的中点，且

  AB

  =

  2

  3

  ，BC=1，AA₁=2，则直线BB₁与AP所成的角为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：88引用：2难度：0.7

  解析

• 4．开普勒第一定律也称椭圆定律、轨道定律，其内容如下：每一行星沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点上．将某行星H看作一个质点，H绕太阳的运动轨迹近似成曲线

  x

  2

  m

  +

  y

  2

  n

  =

  1

  （

  m

  ＞

  n

  ＞

  0

  ）

  ，行星P在运动过程中距离太阳最近的距离称为近日点距离，距离太阳最远的距离称为远日点距离．若行星C的近日点距离和远日点距离之和是20（距离单位：亿千米），近日点距离和远日点距离之积是81，则m+n=（　　）

  A．181

  B．97

  C．52

  D．19
  组卷：72引用：3难度：0.7

  解析

• 5．已知向量

  a

  ，

  b

  满足

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  1

  且

  |

  a

  +

  2

  b

  |

  =

  10

  ，则

  a

  ，

  b

  夹角的余弦值为（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  组卷：151引用：2难度：0.5

  解析

• 6．已知圆台的上下底面半径分别为2和5，且母线与下底面所成为角的正切值为

  4

  3

  ，则该圆台的表面积为（　　）

  A．59π

  B．61π

  C．63π

  D．64π
  组卷：188引用：5难度：0.8

  解析

• 7．已知角

  θ

  ∈

  （

  π

  6

  ，

  π

  2

  ）

  ，且

  cos

  （

  2

  θ

  +

  2

  π

  3

  ）

  =

  -

  3

  5

  ，则

  tan

  （

  θ

  -

  π

  6

  ）

  =（　　）

  A． 4 3

  B． 1 2 或-1

  C． 1 2

  D． 4 3 或 1 2
  组卷：113引用：4难度：0.6

  解析

四、解答题：本大题共6小题，共70分.请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤.

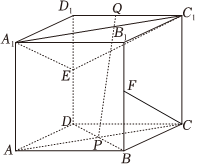• 21．如图，在正方体ABCD-A₁B₁C₁D₁中，点E、F分别为棱DD₁、BB₁的中点，点P为底面对角线AC与BD的交点，点Q是棱D₁C₁上一动点．
  （1）证明：直线CF∥平面A₁EC₁；
  （2）证明：CF⊥PQ．
  组卷：142引用：4难度：0.6

  解析

• 22．已知椭圆E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左右焦点分别为F₁，F₂，过F₂的直线l交椭圆E于P，Q两点（点P位于第三象限），点P关于原点O的对称点为R．当PF₂⊥RF₂时，△PF₂R的面积为1，且|PF₂|+|RF₂|=4．
  （1）求椭圆E的方程；
  （2）若△POQ的面积为

  15

  4

  ，求直线l的方程．
  组卷：75引用：2难度：0.5

  解析