当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省苏州市工业园区星海实验中学九年级（上）开学数学试卷

发布：2024/8/10 10:0:1

一、单选题（本大题共8小题，每小题2分，共16分）

1．若a≠0，下列计算正确的是（　　）
A．（-a）⁰=1 B．a⁶÷a³=a² C．a^-1=-a D．a⁶-a³=a³
组卷：320引用：5难度：0.8
解析
2．下列图形一定既是轴对称图形又是中心对称图形的是（　　）
A．等腰三角形 B．平行四边形 C．菱形 D．直角三角形
组卷：72引用：2难度：0.8
解析
3．若分式
a
2
a
+
b
中的a和b都扩大到原来的n倍，则分式的值（　　）
A．扩大到原来的n倍 B．扩大到原来的2n倍
C．扩大到原来的n²倍 D．不变
组卷：87引用：3难度：0.9
解析
4．下列统计中，能用全面调查的是（　　）
A．检测某城市的空气质量
B．调查全国初中生的视力情况
C．审查某篇文章中的错别字
D．调查央视“新闻联播”的收视率
组卷：75引用：3难度：0.9
解析
5．在函数
y
=
-
m
2
-
3
x
（m为常数）的图象上有三点（-4，y₁），（-2，y₂），（1，y₃），则函数值y₁，y₂，y₃的大小关系为（　　）
A．y₂＜y₁＜y₃ B．y₁＜y₂＜y₃ C．y₃＜y₂＜y₁ D．y₃＜y₁＜y₂
组卷：362引用：4难度：0.6
解析
6．某智能手机代工厂接到生产30万部智能手机的订单，为了满足客户尽快交货的要求，该代工厂增开了一条生产线，实际每月生产能力比原计划提高了50%，结果比原计划提前2个月完成交货，那么原计划每月生产智能手机多少万部？设原计划每月生产智能手机x万部，则根据题意可列方程为（　　）
A．
30
（
1
+
50
%
）
x
-
30
x
=
2
B．
30
（
1
-
50
%
）
x
-
30
x
=
2
C．
30
x
-
30
（
1
-
50
%
）
x
=
2
D．
30
x
-

30
（
1
+
50
%
）
x
=
2
组卷：760引用：5难度：0.7
解析
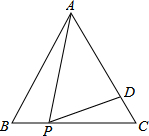7．如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD=60°，BP=2，CD=1，则△ABC的边长为（　　）
A．3 B．4 C．5 D．6
组卷：1062引用：6难度：0.5
解析
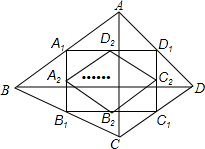8．如图，四边形ABCD中，AC=a,BD=b,且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂，…，如此进行下去，得到四边形A_nB_nC_nD_n．下列结论正确的有（　　）
①四边形A₂B₂C₂D₂是矩形；
②四边形A₄B₄C₄D₄是菱形；
③四边形A₅B₅C₅D₅的周长是
a
+
b
4
；
④四边形A_nB_nC_nD_n的面积是
ab
2
n
+
1
．
A．1个 B．2个 C．3个 D．4个
组卷：461引用：8难度：0.7
解析

二、填空题（本大题共8小题，每小题2分，共16分）

9．要使式子
a
+
3
a
+
1
有意义，则a的取值范围是
．
组卷：108引用：1难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、简答题（本大题共11小题，共68分）

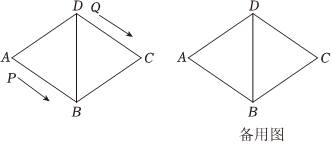26．如图，菱形ABCD的边长为12cm,∠A=60°，动点P从点A出发，沿着线路AB-BD做匀速运动，动点Q从点D同时出发，沿着线路DC-CB-BA做匀速运动．
（1）求BD的长；
（2）已知动点P运动的速度为2cm/s,动点Q运动的速度为2.5cm/s.经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由；
（3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为a cm/s,经过2秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a值．
组卷：61引用：1难度：0.1
解析
27．阅读理解：对于线段MN和点Q，定义：若QM=QN，则称点Q为线段MN的“等距点”；特别地，若∠MQN=90°，则称点Q是线段MN的“完美等距点”．
解决问题：如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（4，0），点P（m,n）是直线y=-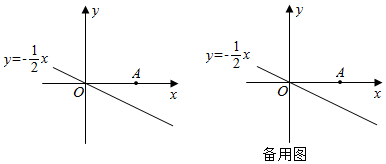
1
2
x上一动点．

（1）已知4个点：B（2，-3）、C（2，-2）、D（-2，2）、E（2，
3
），则线段OA的“等距点”是
，线段OA的“完美等距点”是
．
（2）若OP=
5
，点H在y轴上，且H是线段AP的“等距点”，求点H的坐标；
（3）当m＞0，是否存在这样的点N，使点N是线段OA的“等距点”且为线段OP的“完美等距点”，若存在，求出点P的坐标；若不存在，说明理由．
组卷：700引用：3难度：0.4
解析