当前位置：试卷中心 > 试卷详情

2022-2023学年吉林省松原市乾安县七年级（下）期中数学试卷

发布：2024/6/19 8:0:9

一、选择题（本大题共6小题，每小题2分，共12分）

1．实数25的算术平方根是（　　）
A．±5 B．5 C．
5
D．±
5
组卷：354引用：5难度：0.9
解析
2．下列生活现象中，属于平移的是（　　）
A．升降电梯的上下移动 B．荡秋千运动
C．把打开的课本合上 D．钟摆的摆动
组卷：719引用：8难度：0.8
解析
3．若
x
=
2
y
=
1
是方程ax-3y=1的一个解，则a的值是（　　）
A．2 B．7 C．-1 D．-5
组卷：155引用：5难度：0.9
解析
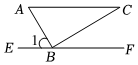4．如图，把一块三角板ABC的直角顶点B放在直线EF上，∠C=30°，AC∥EF，则∠1=（　　）
A．30° B．45° C．60° D．75°
组卷：1419引用：17难度：0.7
解析
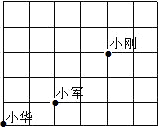5．课间操时，小华、小军、小刚的位置如图1，小华对小刚说，如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么你的位置可以表示成（　　）
A．（5，4） B．（4，5） C．（3，4） D．（4，3）
组卷：4877引用：132难度：0.9
解析
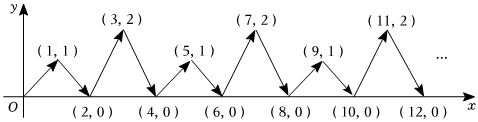
6．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），按这样的运动规律，经过第2023次运动后，动点P的坐标是（　　）
A．（2023，0） B．（2023，1） C．（2023，2） D．（2024，0）
组卷：831引用：8难度：0.6
解析

二、填空题（本大题共8小题，每小题3分，共24分）

7．若一个数的平方根为±8，则这个数的立方根为
．
组卷：216引用：28难度：0.7
解析
8．在电影票上如果将“8排4号”记作（8，4），那么“3排5号”记作
．
组卷：180引用：4难度：0.7
解析
9．已知x,y互为相反数且满足二元一次方程组
2
x
+
5
y
=
k
x
-
3
y
=
16
，则k的值是
．
组卷：785引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

六、解答题（每小题10分，共20分）

26．探究：如图①，AB∥CD∥EF，点G、P、H分别在直线AB、CD、EF上，连接PG、PH，当点P在直线GH的左侧时，试说明∠AGP+∠EHP=∠GPH．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式数学符号）．

（1）填空：如图①，
∵AB∥CD（已知），
∴∠AGP
∠GPD．
∵CD∥EF，
∴∠DPH=∠EHP（
），
∵∠GPD+∠DPH=∠GPH，
∴∠AGP+∠EHP=∠GPH（
）．
（2）拓展：将图①的点P移动到直线GH的右侧，其他条件不变，如图②．试探究∠AGP，∠EHP、∠GPH之间的关系，并说明理由．
（3）应用：如图③，AB∥CD∥EF，点G、H分别在直线AB、EF上，点Q是直线CD上的一个动点，且不在直线GH上，连接QG、QH．若∠GQH=70°，请求出∠AGQ+∠EHQ的度数．
组卷：30引用：1难度：0.5
解析
27．如图，以直角三角形AOC的直角顶点O为原点，以OC，OA所在直线为x轴，y轴建立平面直角坐标系，点A（0，a），C（c,0）满足
2
c
-
a
+
|
c
-
6
|
=
0
．

（1）C点的坐标为
；A点的坐标为
．
（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（3，6），设运动时间为t（t＞0）秒，问：是否存在这样的t使S_△ODP=S_△ODQ？若存在，请求出t的值；若不存在，请说明理由．
（3）点F是线段AC上一点，满足∠FOC=∠FCO，点G是第二象限中一点，连OG，OA平分∠FOG．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，探究∠OHC，∠ACE，∠FOG之间的数量关系．
组卷：140引用：4难度：0.3
解析