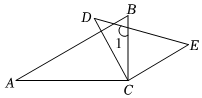
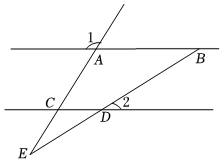
探究:如图①,AB∥CD∥EF,点G、P、H分别在直线AB、CD、EF上,连接PG、PH,当点P在直线GH的左侧时,试说明∠AGP+∠EHP=∠GPH.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式数学符号).

(1)填空:如图①,
∵AB∥CD(已知),
∴∠AGP ==∠GPD.
∵CD∥EF,
∴∠DPH=∠EHP( 两直线平行,内错角相等两直线平行,内错角相等),
∵∠GPD+∠DPH=∠GPH,
∴∠AGP+∠EHP=∠GPH( 等量代换等量代换).
(2)拓展:将图①的点P移动到直线GH的右侧,其他条件不变,如图②.试探究∠AGP,∠EHP、∠GPH之间的关系,并说明理由.
(3)应用:如图③,AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连接QG、QH.若∠GQH=70°,请求出∠AGQ+∠EHQ的度数.
【考点】平行线的性质.
【答案】=;两直线平行,内错角相等;等量代换
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/18 8:0:10组卷:30引用:1难度:0.5