2022-2023学年北京五十五中高二（下）调研数学试卷（3月份）

一、（共10小题；共40分）

• 1．在等差数列{a_n}中，a₁+a₉=10，则a₅的值为（　　）

  A．5

  B．6

  C．8

  D．10
  组卷：1219引用：59难度：0.9

  解析

• 2．已知函数

  f

  （

  x

  ）

  =

  1

  -

  x

  ，则f'（x）=（　　）

  A． - 1 2 1 - x

  B． 1 2 1 - x

  C． - 2 1 - x

  D． 2 1 - x
  组卷：223引用：2难度：0.9

  解析

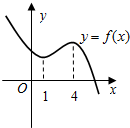• 3．设函数f（x）的图象如图所示，则导函数f′（x）的图象可能为（　　）

  A．	B．
  C．	D．
  组卷：320引用：13难度：0.9

  解析

• 4．在等比数列{a_n}中，公比是q,则“q＞1”是“

  a

  n

  +

  1

  ＞

  a

  n

  （

  n

  ∈

  N

  *

  ）

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：320引用：2难度：0.8

  解析

• 5．“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等于

  12

  2

  ．若第一个单音的频率为f,则第八个单音的频率为（　　）

  A． 3 2 f

  B． 3 2 2 f

  C． 12 2 5 f

  D． 12 2 7 f
  组卷：3811引用：28难度：0.9

  解析

• 6．若函数f（x）=x³-tx²+3x在区间R上单调递增，则实数t的取值范围是（　　）

  A．（-∞，-3]

  B．[-3，3]

  C．（-3，3）

  D．[3，+∞）
  组卷：153引用：3难度：0.6

  解析

• 7．若直线y=kx是函数f（x）=lnx切线，则实数k的值是（　　）

  A． 1 e 2

  B． 1 e

  C．1

  D．-1
  组卷：112引用：2难度：0.7

  解析

三、解答题（共6小题；共85分）

• 20．已知函数f（x）=-x²+ax-ln（x+1）．
  （1）若a=1，求函数f（x）的极值点．
  （2）若函数f（x）既存在极大值又存在极小值，求实数a的取值范围．
  组卷：158引用：3难度：0.5

  解析

• 21．若有穷数列{a_n}满足：0≤a₁＜a₂＜…＜a_k（k∈N^*，k≥3）且对任意的i,j（1≤i≤j≤k），a_j+a_i与a_j-a_i至少有一个是数列{a_n}中的项，则称数列{a_n}具有性质P．
  （1）判断数列1，2，4，8是否具有性质P，并说明理由；
  （2）设项数为k（k∈N^*，k≥3）的数列{a_n}具有性质P，求证：ka_k=2（a₁+a₂+…+a_k-1+a_k）；
  （3）若项数为k（k∈N^*，k≥3）的数列{a_n}具有性质P，写出一个当k=4时，{a_n}不是等差数列的例子，并证明当k＞4时，数列{a_n}是等差数列．
  组卷：269引用：2难度：0.1

  解析