2023-2024学年江苏省盐城市东台中学高三（上）第一次段考数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，则∁_U（A∪B）=（　　）

  A．（-∞，-1]∪（2，+∞）	B．（-∞，-1）∪[2，+∞）
  C．[3，+∞）	D．（3，+∞）
  组卷：441引用：10难度：0.8

  解析

• 2．设命题p：∀n∈N，n²＜3n+4，则p的否定为（　　）

  A．∀n∈N，n2＞3n+4	B．∀n∈N，n2≤3n+4
  C．∃n∈N，n2≥3n+4	D．∃n∈N，n2＞3n+4
  组卷：255引用：12难度：0.8

  解析

• 3．已知a,b∈R，则“a＞b＞2”是“a-2＞|b-2|”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：199引用：4难度：0.7

  解析

• 4．设

  a

  =

  1

  2

  ，

  b

  =

  sin

  1

  2

  ，

  c

  =

  lo

  g

  2

  3

  ，则（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．b＜a＜c

  D．b＜c＜a
  组卷：112引用：3难度：0.8

  解析

• 5．函数y=（2^x-2^-x）cosx在区间[-2，2]上的图象大致为（　　）

  A．	B．
  C．	D．
  组卷：134引用：13难度：0.7

  解析

• 6．牛顿曾经提出了常温环境下的温度冷却模型：

  θ

  =

  （

  θ

  1

  -

  θ

  0

  ）

  e

  -

  kt

  +

  θ

  0

  ，其中t为时间（单位：min），θ₀为环境温度，θ₁为物体初始温度，θ为冷却后温度．假设在室内温度为20°C的情况下，一杯饮料由100°C降低到60°C需要20min,则此饮料从60°C降低到40°C需要（　　）

  A．10min

  B．20min

  C．40min

  D．30min
  组卷：233引用：5难度：0.5

  解析

• 7．设函数f（x）=3^x+b,函数f（x）的图像经过第一、三、四象限，则g（b）=f（b）-f（b-1）的取值范围为（　　）

  A． （ 0 ， 2 9 ）

  B． （ - ∞ ， 2 9 ）

  C． （ - ∞ ， 2 3 ）

  D． （ 0 ， 2 3 ）
  组卷：279引用：4难度：0.7

  解析

四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

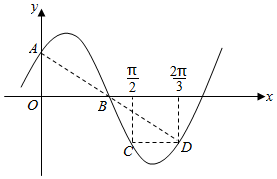• 21．如图，已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π），点A，B分别是f（x）的图象与y轴、x轴的交点，C，D分别是f（x）的图象上横坐标为

  π

  2

  、

  2

  π

  3

  的两点，CD∥x轴，A，B，D共线．
  （Ⅰ）求ω，φ的值；
  （Ⅱ）若关于x的方程f（x）=k+sin2x在区间[

  π

  12

  ，

  π

  2

  ]上恰有唯一实根，求实数k的取值范围．
  组卷：872引用：3难度：0.1

  解析

• 22．已知函数f（x）=

  - ln （ 1 - | x + 1 | ） ，- 2 ＜ x ＜ 0

  | lnx | ， x ＞ 0

  ．
  （1）求函数f（x）的单调递增区间；
  （2）若关于x的方程f（2x-1）=m有4个不同的解，记为x₁，x₂，x₃，x₄（x₁＜x₂＜x₃＜x₄），且λ•

  x

  3

  x

  4

  -x₁x₂＞

  1

  5

  恒成立，求λ的取值范围．
  组卷：125引用：3难度：0.3

  解析