2021-2022学年四川省达州市宣汉县土黄中学高一（下）期中数学试卷

一、选择题：本大题共12小题，每一小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={0，1，2，4}，B={x|0＜x＜4}，则A∩B=（　　）

  A．{1，2}

  B．{1，4}

  C．{2，4}

  D．{1，2，4}
  组卷：62引用：3难度：0.9

  解析

• 2．若向量

  a

  =

  （

  1

  ，-

  3

  ）

  ，

  b

  =

  （

  3

  ，-

  8

  ）

  ，则

  2

  （

  a

  -

  b

  ）

  =（　　）

  A．（-4，10）

  B．（-2，5）

  C．（4，5）

  D．（8，10）
  组卷：563引用：5难度：0.9

  解析

• 3．已知斐波拉契数列（Fibonaccisequence）{F_n}满足F_n=F_n-1+F_n-2（n＞2），F₁=F₂=1，则F₆等于（　　）

  A．3

  B．5

  C．8

  D．13
  组卷：76引用：2难度：0.8

  解析

• 4．函数y=2^x-sin2x的图象大致是（　　）

  A．	B．
  C．	D．
  组卷：391引用：4难度：0.7

  解析

• 5．在△ABC中，A=30°，b=

  3

  ，c=1，则a=（　　）

  A．2

  B． 3

  C． 2

  D．1
  组卷：352引用：4难度：0.9

  解析

• 6．已知数列{a_n}为等差数列，且a₁+a₇+a₁₃=π，则tan（a₂+a₁₂）的值为（　　）

  A． 3

  B． - 3

  C． ± 3

  D． - 3 3
  组卷：566引用：29难度：0.9

  解析

• 7．等差数列{a_n}和{b_n}的前n项和分别为S_n与T_n，对一切自然数n∈N*，都有

  S

  n

  T

  n

  =

  2

  n

  3

  n

  +

  1

  ，则

  a

  5

  b

  5

  等于（　　）

  A． 2 3

  B． 9 14

  C． 20 31

  D． 11 17
  组卷：172引用：27难度：0.7

  解析

三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

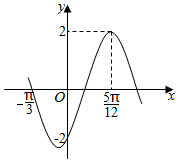• 21．已知函数

  f

  （

  x

  ）

  =

  2

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，-

  π

  2

  ＜

  φ

  ＜

  π

  2

  ）

  的部分图象如图所示．
  （1）求函数f（x）的解析式；
  （2）在锐角ABC中，角A，B，C所对的边分别为a,b,c,若

  f

  （

  A

  ）

  =

  3

  ，b=2，且ABC的面积为

  3

  3

  2

  ，求a.
  组卷：229引用：8难度：0.6

  解析

• 22．设{a_n}是公差大于1的等差数列，数列{b_n}满足

  b

  2

  n

  =b_n+1•b_n-1（n≥2）．已知a₁=1，b₁=4，b₂=a₂+a₃，2a₃是b₁和b₃的等差中项．
  （1）求数列{a_n}和数列{b_n}的通项公式；
  （2）设c_n=

  a

  n

  b

  n

  ，且数列{c_n}的前n项和为T_n，若对任意的n∈N^*，不等式T_n＜a²-

  1

  2

  a恒成立，求a的取值范围．
  组卷：110引用：4难度：0.5

  解析