2022-2023学年浙江省台州市黄岩区七年级（下）期末数学试卷

一、选择题（本题有10小题，每小题3分，共30分、请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）

• 1．点P（-1，3）所在的象限为（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：169引用：6难度：0.7

  解析

• 2．如图，OA⊥OB，OC是一条射线．若∠AOC=120°，则∠BOC的度数是（　　）

  A．60°

  B．45°

  C．30°

  D．20°
  组卷：31引用：1难度：0.7

  解析

• 3．正方形的面积是13，估计它的边长大小在（　　）

  A．2与3之间

  B．3与4之间

  C．4与5之间

  D．5与6之间
  组卷：167引用：5难度：0.7

  解析

• 4．疫情过后，为了解某市600万民众的身体健康状况，从中任意抽取1000人进行调查．在这个问题中，这1000人的身体健康状况是（　　）

  A．样本

  B．个体

  C．总体

  D．样本容量
  组卷：32引用：1难度：0.7

  解析

• 5．若

  x = 2

  y = 1

  是方程3x-ky=10的解，则k的值是（　　）

  A．一 7 2

  B．4

  C．一4

  D．16
  组卷：159引用：2难度：0.9

  解析

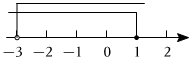• 6．两个不等式的解集在数轴上表示如图，则这两个不等式组成的不等式组的解集是（　　）

  A．x＞-3或x≤1

  B．-3＜x≤1

  C．-3＜x＜1

  D．-3≤x＜1
  组卷：66引用：1难度：0.8

  解析

• 7．下列命题中，真命题的是（　　）

  A．如果两个角的和等于90°，那么这两个角互为补角

  B．内错角相等

  C．如果两条直线平行，那么同旁内角相等

  D．有三条直线a,b,c,如果a∥b,b∥c,那么a∥c
  组卷：62引用：1难度：0.7

  解析

• 8．一次智力测验，有20道选择题．评分标准是：对1题给5分，错1题扣2分，不答题不给分也不扣分．小明有两道题未答，要使总分不低于60分，那么小明至少答对的题数是（　　）

  A．15道

  B．14道

  C．13道

  D．12道
  组卷：674引用：2难度：0.5

  解析

三、解答题（本题有8大题，第17，18题每题6分，第19～22题每题8分，第23题10分，第24题12分，共66分）

• 23．已知直线AC∥OB，OA⊥OB，垂足为点O，点A，B分别在直线OA，OB上．点P是平面上任一点，连接PA，PB．
  
  （1）当点P在如图1所示位置时，∠OBP=30°，∠OAP=20°，则∠APB=

  °；
  （2）当点P移动到如图2所示位置时，求∠OBP，∠OAP，∠APB之间的数量关系，并说明理由；
  （3）如图3，在（2）的条件下分别作∠OBP，∠OAP的角平分线交于点Q，
  ①若∠P=60°，求∠Q的度数；
  ②请直接写出∠P和∠Q的数量关系．
  组卷：229引用：1难度：0.5

  解析

• 24．定义：已知平面上两点A（x₁，y₁），B（x₂，y₂），称d（A，B）=|x₁-x₂|+|y₁-y₂|为A，B两点之间的折线距离．例如点M（2，-3）与点N（5，2）之间的折线距离为d（M，N）=|2-5|+|-3-2|=3+5=8．如图，已知平面直角坐标系中点A（2，1），B（-1，0）．
  
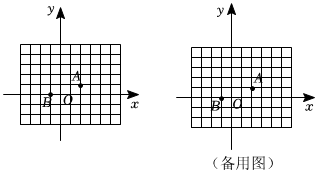
  （1）d（A，B）=

  ；
  （2）过点B作直线l平行于y轴，求直线l上与点A的折线距离为5的点的坐标；
  （3）已知点N（n,n），且d（A，N）＜2，求n的取值范围；
  （4）已知平面上点P与原点O的折线距离为3，即d（P，O）=3，直接写出所有满足条件的点P围成的图形面积．
  组卷：90引用：2难度：0.5

  解析