当前位置：试卷中心 > 试卷详情

2023-2024学年广东省深圳市宝安区新华中学九年级（上）诊断数学试卷（10月份）

发布：2024/9/9 10:0:8

一.选择题（共10小题，每题3分共30分）

1．下列方程中，是关于x的一元二次方程的是（　　）
A．x+3x-6=12 B．2x+y=8 C．x²+3x=2 D．
2
x
-
1
x
=
6
组卷：140引用：4难度：0.9
解析
2．用配方法解一元二次方程x²-6x+8=0配方后得到的方程是（　　）
A．（x+6）²=28 B．（x-6）²=28 C．（x+3）²=1 D．（x-3）²=1
组卷：2654引用：53难度：0.7
解析
3．若菱形的周长为100cm,有一条对角线为48cm,则菱形的面积为（　　）
A．336cm² B．480cm² C．300cm² D．168cm²
组卷：744引用：5难度：0.6
解析
4．下列方程中有两个相等的实数根的是（　　）
A．x²-2x-1=0 B．
x
2
-
x
+
1
4
=
0
C．x²+3x+5=0 D．2x²-3x+1=0
组卷：103引用：2难度：0.5
解析
5．在四边形ABCD中，AD∥BC，AB=CD．下列说法能使四边形ABCD为矩形的是（　　）
A．AB∥CD B．AD=BC C．∠A=∠B D．∠A=∠D
组卷：2555引用：24难度：0.5
解析
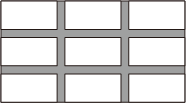6．如图，在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是3600m²，则小路的宽是（　　）
A．5m B．70m C．5m或70m D．10m
组卷：3237引用：28难度：0.7
解析
7．向阳村2010年的人均年收入为12000元，2012年的人均年收入为14520元．设人均年收入的平均增长率为x,则下列所列的方程中正确的是（　　）
A．14520（1-x²）=12000 B．12000（1+x）²=14520
C．14520（1+x）²=12000 D．12000（1-x）²=14520
组卷：595引用：13难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共7小题，共55分）

21．【阅读材料】配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
我们定义：一个整数能表示成a²+b²（a,b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5=2²+1²，所以5是“完美数”．
【解决问题】
（1）数53
“完美数”（填“是”或“不是”）；
【探究问题】
（2）已知x²+y²-4x+2y+5=0，则x+y=
；
（3）已知S=2x²+y²+2xy+12x+k（x,y 是整数，k是常数），要使S为“完美数”，试求出符合条件的k值，并说明理由；
【拓展结论】
（4）已知实数x、y满足
-
x
2
+
7
2
x
+
y
-
3
=
0
，求x-2y的最大值．
组卷：1495引用：5难度：0.5
解析
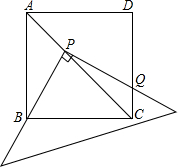22．如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．
探究：设A、P两点间的距离为x.
（1）当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；
（2）当点Q在边CD上时，设四边形PBCQ的面积为y,求y与x之间的函数关系，并写出函数自变量x的取值范围；
（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x值，如果不可能，试说明理由．
组卷：2787引用：19难度：0.5
解析