2022-2023学年广西南宁市上林县九年级（上）期中数学试卷

一．选择题（每题3分，共36分）

• 1．气象局调查了甲、乙两个城市连续四年的降水量，它们的平均降水量都是323毫米，方差分别是S_甲²=3.2，S_乙²=5.2，则这两个城市年降水量最稳定的是（　　）

  A．甲

  B．乙

  C．都一样

  D．无法比较
  组卷：1引用：1难度：0.7

  解析

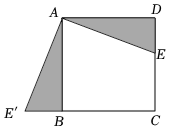• 2．如图，E是正方形ABCD中CD边上任意一点，以点A为旋转中心，把△ADE顺时针旋转90°得到△ABE'，则∠E'AE的度数是（　　）

  A．45°

  B．60°

  C．75°

  D．90°
  组卷：147引用：3难度：0.7

  解析

• 3．抛物线y=-（x-1）²+3的顶点坐标是（　　）

  A．（1，3）

  B．（-1，3）

  C．（-1，-3）

  D．（1，-3）
  组卷：1053引用：15难度：0.9

  解析

• 4．方程x²+3x-4=0的两根分别为x₁，x₂，则x₁+x₂等于（　　）

  A．-4

  B．4

  C．-3

  D．3
  组卷：197引用：4难度：0.6

  解析

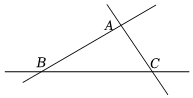• 5．如图，三条公路两两相交，现计划在△ABC中内部修建一个探照灯，要求探照灯的位置到这三条公路的距离都相等，则探照灯位置是△ABC（　　）的交点．

  A．三条角平分线	B．三条中线
  C．三条高的交点	D．三条垂直平分线
  组卷：662引用：5难度：0.7

  解析

• 6．关于抛物线y=x²-4x+4，下列说法错误的是（　　）

  A．开口向上

  B．与x轴有两个重合的交点

  C．对称轴是直线x=2

  D．当x＞2时，y随x的增大而减小
  组卷：158引用：6难度：0.5

  解析

• 7．分式方程

  1

  x

  -

  3

  +1=

  x

  3

  -

  x

  的解为（　　）

  A．无解

  B．x=1

  C．x=-1

  D．x=-2
  组卷：700引用：5难度：0.7

  解析

• 8．抛物线y=2x²向左平移1个单位，再向下平移3个单位，则平移后的抛物线的解析式为（　　）

  A．y=2（x+1）2+3	B．y=2（x+1）2-3
  C．y=2（x-1）2-3	D．y=2（x-1）2+3
  组卷：583引用：26难度：0.9

  解析

三．解答题（共72分）

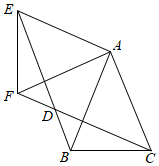• 25．如图，在等腰直角△ACF中，AC=AF，△ABE是由△ACF绕点A按顺时针方向旋转得到的，连接EF、BC．
  （1）求证：EF=BC；
  （2）当旋转角为40°时，求∠BCF的度数．
  组卷：242引用：8难度：0.4

  解析

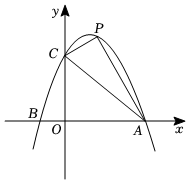• 26．如图，在平面直角坐标系中，直线y=-

  3

  4

  x+3与x轴交于点A，与y轴交于点C．抛物线y=-

  1

  4

  x

  2

  +bx+c经过点A、C．
  （1）求抛物线解析式及顶点M坐标；
  （2）P为抛物线第一象限内一点，使得△PAC面积最大，求△PAC面积的最大值及此时点P的坐标；
  （3）当m≤x≤m+1时，（1）中二次函数有最大值为-2，求m的值．
  组卷：731引用：5难度：0.6

  解析