2023-2024学年河南省焦作市博爱一中高二(上)月考数学试卷(10月份)
发布:2024/9/21 10:0:8
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知A={1,x,y},B={1,x2,2y},若A=B,则x-y=( )
组卷:1053引用:17难度:0.7 -
2.已知函数
,f(x)=x+1x,则|f(x1)-f(x2)|的最大值为( )x1,x2∈[12,3]组卷:78引用:1难度:0.6 -
3.已知点
是角α终边上一点,则sinα=( )P(cosπ3,1)组卷:405引用:8难度:0.7 -
4.已知平面向量
,AB=(1,2),则向量AC=(3,4)的模是( )CB组卷:1060引用:7难度:0.9 -
5.已知球O是正三棱锥A-BCD(底面是正三角形,顶点在底面的射影为底面中心)的外接球,BC=3,AB=
,点E在线段BD上,且BD=3BE.过点E作球O的截面,则所得截面面积的最小值是( )23组卷:200引用:3难度:0.6 -
6.某大街在甲、乙、丙三处设有红绿灯,汽车在这三处遇到绿灯的概率分别是
,13,12,则汽车在这三处共遇到两次绿灯的概率为( )23组卷:229引用:6难度:0.7 -
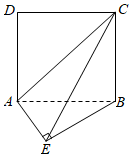 7.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )组卷:211引用:11难度:0.7
7.如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )组卷:211引用:11难度:0.7
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知两条直线l1:ax-by+4=0,l2:(a-1)x+y+b=0,求满足下列条件的a,b值.
(Ⅰ)l1⊥l2且l1过点(-3,-1);
(Ⅱ)l1∥l2且原点到这两直线的距离相等.组卷:1193引用:22难度:0.5 -
22.已知椭圆C:
+x2a2=1(a>b>0)的离心率为y2b2,且过点A(2,1).22
(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.组卷:8700引用:28难度:0.2


