2023-2024学年江西省宜春市上高二中高二（上）期中数学试卷

一、单选题（每小题5分，共40分）

• 1．已知复数

  z

  =

  1

  -

  3

  i

  ，则

  |

  z

  |

  z

  •

  z

  -

  2

  z

  =（　　）

  A． 1 4 - 3 4 i

  B． 1 2 - 3 2 i

  C． 1 4 + 3 4 i

  D． 1 2 + 3 2 i
  组卷：187引用：7难度：0.8

  解析

• 2．两条平行直线3x+4y-12=0与ax+8y+11=0之间的距离为（　　）

  A． 23 5

  B． 23 10

  C．7

  D． 7 2
  组卷：803引用：40难度：0.9

  解析

• 3．已知某圆锥的高为4，其内切球的体积为

  4

  3

  π

  ，则该圆锥的侧面积S=（　　）

  A．π

  B．3π

  C．6π

  D．12π
  组卷：80引用：1难度：0.7

  解析

• 4．若直线l的斜率

  k

  ∈

  （

  -

  1

  ，

  3

  ）

  ，则直线l的倾斜角的取值范围是（　　）

  A． （ π 3 ， 3 π 4 ）	B． [ 0 ， π 3 ） ∪ （ 3 π 4 ， π ）
  C． （ π 6 ， 2 π 3 ）	D． [ 0 ， π 6 ） ∪ （ 3 π 4 ， π ）
  组卷：250引用：11难度：0.8

  解析

• 5．已知

  a

  =（2，1，-3），

  b

  =（-1，2，3），

  c

  =（7，6，λ），若

  a

  ，

  b

  ，

  c

  共面，则λ等于（　　）

  A．-3

  B．3

  C．-9

  D．9
  组卷：660引用：18难度：0.8

  解析

• 6．已知圆C₁：（x-2m）²+（y-2m）²=9（m-2）与圆C₂：x²+y²-8x-8y+34-m=0，则“m=4”是“圆C₁与圆C₂外切”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：63引用：5难度：0.6

  解析

• 7．已知圆

  C

  1

  ：

  x

  2

  +

  y

  2

  -

  kx

  +

  2

  y

  =

  0

  与圆

  C

  2

  ：

  x

  2

  +

  y

  2

  +

  ky

  -

  2

  =

  0

  的公共弦所在直线经过定点P，且点P在直线mx-ny-2=0上，则m²+2n的取值范围是（　　）

  A．[3，+∞）

  B．[2，+∞）

  C．[0，3]

  D．[0，4]
  组卷：307引用：4难度：0.7

  解析

四、解答题（17题10分，18-22题每题12分，共70分）

• 21．已知圆心在x轴上的圆C与直线l：4x+3y-6=0切于点

  M

  （

  3

  5

  ，

  6

  5

  ）

  ．
  （1）求圆C的标准方程；
  （2）已知N（2，1），经过原点且斜率为正数的直线l₁与圆C交于P（x₁，y₁），Q（x₂，y₂）．求|PN|²+|QN|²的最大值．
  组卷：148引用：4难度：0.6

  解析

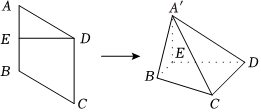• 22．如图，菱形ABCD的边长为2，∠BAD=60°，E为AB的中点．将△ADE沿DE折起，使A到达A′，连接A′B，A′C，得到四棱锥A′-BCDE．
  （1）证明：DE⊥A′B；
  （2）当二面角A′-DE-B的平面角在

  [

  π

  3

  ，

  2

  π

  3

  ]

  内变化时，求直线A′C与平面A′DE所成角的正弦值的取值范围．
  组卷：51引用：4难度：0.4

  解析