当前位置：试卷中心 > 试卷详情

2023-2024学年浙江省台州市路桥区东方理想学校九年级（上）月考数学试卷（9月份）

发布：2024/8/30 3:0:9

一、选择题：（本大题共10小题，共30分）

1．下列各图案中，属于中心对称图形的是（　　）
A． B． C． D．
组卷：123引用：4难度：0.9
解析
2．二次函数y=（x+2）²-3的顶点坐标是（　　）
A．（2，-3） B．（-2，-3） C．（2，3） D．（-2，3）
组卷：734引用：23难度：0.6
解析
3．已知OA=4，以O为圆心，r为半径作⊙O．若使点A在⊙O内，则r的值可以是（　　）
A．2 B．3 C．4 D．5
组卷：714引用：22难度：0.8
解析
4．数-1，0，1，3中，是一元二次方程x²-3x+2=0的解的是（　　）
A．-1 B．0 C．1 D．3
组卷：9引用：2难度：0.5
解析
5．如图，CD为⊙O的直径，弦AB⊥CD于E，OE=12，CD=26，那么弦AB的长为（　　）
A．5 B．10 C．12 D．13
组卷：296引用：4难度：0.6
解析
6．将抛物线y=3x²向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（　　）
A．y=3（x+2）²+3 B．y=3（x-2）²+3
C．y=3（x+2）²-3 D．y=3（x-2）²-3
组卷：962引用：110难度：0.9
解析
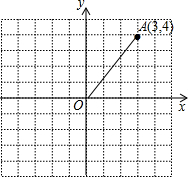7．如图，在平面直角坐标系中，A点坐标为（3，4），将OA绕原点O逆时针旋转90°得到OA′，则点A′的坐标是（　　）
A．（-4，3） B．（-3，4） C．（3，-4） D．（4，-3）
组卷：205引用：27难度：0.9
解析
8．若关于x的一元二次方程（m+1）x²-x+m²-m-2=0有一根为0，则m的值为（　　）
A．2 B．-1 C．2或-1 D．1或-2
组卷：675引用：6难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（本大题共8小题，共66分）

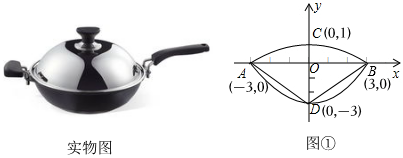23．我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形，不妨简称为“锅线”，锅口直径为6dm,锅深3dm,锅盖高1dm（锅口直径与锅盖直径视为相同），建立直角坐标系如图①所示，如果把锅纵断面的抛物线记为C₁，把锅盖纵断面的抛物线记为C₂．
（1）求C₁和C₂的解析式；
（2）如果炒菜时锅的水位高度是1dm,求此时水面的直径；
（3）如果将一个底面直径为3dm,高度为3.2dm的圆柱形器皿放入炒菜锅内蒸食物，锅盖能否正常盖上？请说明理由．
组卷：766引用：9难度：0.3
解析
24．如图1：在Rt△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），试探索AD，BD，CD之间满足的等量关系，并证明你的结论．
小明同学的思路是这样的：将线段AD绕点A逆时针旋转90°，得到线段AE，连接EC，DE．继续推理就可以使问题得到解决．
（1）请根据小明的思路，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；
（2）如图2，在Rt△ABC中，AB=AC，D为△ABC外的一点，且∠ADC=45°，线段AD，BD，CD之间满足的等量关系又是如何的，请证明你的结论；
（3）如图3，已知AB是⊙O的直径，点C，D是⊙O上的点，且∠ADC=45°．
①若AD=6，BD=8，求弦CD的长为
；
②若AD+BD=14，求
AD
•
（
BD
+
2
2
CD
）
的最大值，并求出此时⊙O的半径．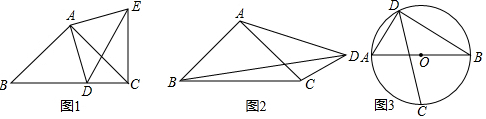
组卷：583引用：3难度：0.1
解析