当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省金华市东阳市江北中学八年级（上）第三次月考数学试卷

发布：2024/8/16 5:0:1

一、选择题

1．如图，为了估计一池塘岸边两点A，B之间的距离，小颖同学在池塘一侧选取了一点P，测得PA=100m,PB=90m,那么点A与点B之间的距离可能是（　　）
A．10m B．120m C．190m D．220m
组卷：377引用：15难度：0.7
解析
2．下列描述不能确定具体位置的是（　　）
A．某电影院6排7座 B．岳麓山北偏东40度
C．劳动西路428号 D．北纬28度，东经112度
组卷：703引用：2难度：0.7
解析
3．A疫苗冷库储藏温度要求为0℃～6℃，B疫苗冷库储藏温度要求为2℃～8℃，若需要将A，B两种疫苗储藏在一起，则冷库储藏温度要求为（　　）
A．0℃～2℃ B．0℃～8℃ C．2℃～6℃ D．6℃～8℃
组卷：335引用：4难度：0.7
解析
4．如图，点E、H、G、N共线，∠E=∠N，EF=NM，添加一个条件，不能判断△EFG≌△NMH的是（　　）
A．EH=NG B．∠F=∠M C．FG=MH D．FG∥HM
组卷：960引用：19难度：0.7
解析
5．若函数y=（m-1）x^|m|-5是一次函数，则m的值为（　　）
A．±1 B．-1 C．1 D．2
组卷：10493引用：81难度：0.9
解析
6．下列命题的逆命题不正确的是（　　）
A．直角三角形的两锐角互余
B．相等的两个角就一定是对顶角
C．若a²=b²，则a=b
D．全等三角形的三个对应角相等
组卷：393引用：5难度：0.5
解析
7．把一些书分给几名同学，若________；若每人分11本，则不够．依题意，设有x名同学，可列不等式9x+7＜11x,则横线上的信息可以是（　　）
A．每人分7本，则可多分9个人
B．每人分7本，则剩余9本
C．每人分9本，则剩余7本
D．其中一个人分7本，则其他同学每人可分9本
组卷：1850引用：26难度：0.7
解析
8．如图，点M是∠AOB平分线上的一点，点P、点Q分别在射线OA、射线OB上，满足OP=2OQ，若△OMP的面积是2，则△OQM的面积是（　　）
A．1 B．2 C．3 D．4
组卷：643引用：6难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

23．问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系，小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是
；
探索延伸：如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠EAF=
1
2
∠BAD，上述结论是否仍然成立，并说明理由；
实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以70海里/小时的速度前进，舰艇乙沿北偏东50°的方向以90海里/小时的速度，前进2小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．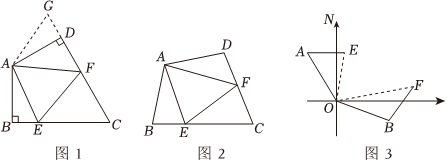
组卷：5473引用：9难度：0.3
解析
24．在平面直角坐标系xOy中，直线l：y=kx+1（k≠0）与直线x=k,直线y=-k分别交于点A，B，直线x=k与直线y=-k交于点C．
（1）求直线l与y轴的交点坐标；
（2）横、纵坐标都是整数的点叫做整点，记线段AB，BC，CA围成的区域（不含边界）为W．
①当k=2时，结合函数图象，求区域W内的整点个数；
②若区域W内没有整点，直接写出k的取值范围．
组卷：4369引用：19难度：0.6
解析