2022-2023学年湖南省长沙市开福区青竹湖湘一外国语学校七年级(下)期末数学试卷
发布:2024/7/9 8:0:8
一、选择题(10个小题,每小题3分,共30分)
-
1.在有理数1,0,
,-2中,是负数的为( )12组卷:1262引用:8难度:0.8 -
2.点P(1,2)所在的象限是( )
组卷:256引用:8难度:0.7 -
3.下列各组线段中,能构成三角形的是( )
组卷:1843引用:19难度:0.7 -
4.有大小两个盛酒的桶,已知2个大桶和5个小桶可以盛酒3斛(斛,古代一种容器单位).3个大桶和6个小桶盛酒4斛,设1个大桶盛酒x斛,1个小桶酒y斛,可列方程组为( )
组卷:439引用:6难度:0.6 -
5.下列问题中,最适合采用全面调查方式的是( )
组卷:337引用:5难度:0.9 -
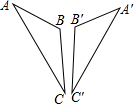 6.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )组卷:1201引用:13难度:0.7
6.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=( )组卷:1201引用:13难度:0.7 -
7.若a>b,则下列不等式不一定成立的是( )
组卷:487引用:15难度:0.8 -
8.语句“x的
与x的和超过2”可以表示为( )13组卷:684引用:10难度:0.6
三、解答题(共9个小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分。解答应写出必要的文字说明、证明过程或演算步骤)
-
24.我们定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“梦想解”.
例:已知方程2x-3=1与不等式x+3>0,方程的解为x=2,使得不等式也成立,则称“x=2”为方程2x-3=1和不等式x+3>0的“梦想解”
(1)已知①,②2(x+3)<4,③x-12>32,试判断方程2x+3=1解是否为它与它们中某个不等式的“梦想解”;x-12<3
(2)若关于x,y的二元一次方程组的解是不等式组3x-2y=m+22x-y=m-5的梦想解,且m为整数,求m的值.x+y>-5x+y<1
(3)若关于x的方程x+4=3m的解是关于x的不等式组的“梦想解”,且此时不等式组有7个整数解,试求m的取值范围.x>m-1x-1≤3m组卷:1481引用:7难度:0.6 -
25.如图,A(0,m),B(n,0),满足
,点P是x轴上的一个动点,点C是AB的中点,连接PC,将PC绕点C逆时针旋转90°到CE.m-4+(n-4)2=0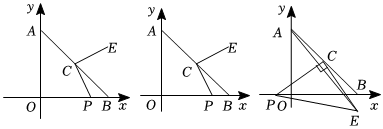
(1)求A、B、C三点的坐标;
(2)当点P在线段OB上或OB延长线上时,若OP=3BP,求点E的坐标;
(3)当点P在线段BO的延长线上时,连接AE,若S△ACE=a•S△PBC,a的值在变化,求点E的运动路径长度.13≤a≤34组卷:520引用:2难度:0.3


