当前位置：试卷中心 > 试卷详情

2022-2023学年北京市清华大学附中非马班高一（上）期末数学试卷

发布：2024/4/20 14:35:0

1．设集合A={x|x≤1}，B={x|2^x≥1}，则A∩B等于（　　）
A．{x|x≤0} B．{x|x≤1} C．{x|x≥0} D．{x|0≤x≤1}
组卷：96引用：1难度：0.8
解析
2．若点P（1，-2）在角α的终边上，则sinα=（　　）
A．-2 B．
-
1
2
C．
-
2
5
5
D．
5
5
组卷：459引用：1难度：0.9
解析
3．计算：2log₃6-log₃4=（　　）
A．1 B．2 C．3 D．6
组卷：1045引用：2难度：0.9
解析
4．要得到函数
y
=
sin
（
2
x
+
π
4
）
，只需将函数y=sin2x的图象（　　）
A．向左平移
π
8
个单位长度 B．向右平移
π
8
个单位长度
C．向左平移
π
4
个单位长度 D．向右平移
π
4
个单位长度
组卷：938引用：4难度：0.9
解析
5．已知a=lg12，b=log_0.25，c=4^-0.5，则a,b,c的大小关系为（　　）
A．a＞b＞c B．c＞b＞a C．a＞c＞b D．b＞a＞c
组卷：425引用：2难度：0.9
解析
6．下列函数中，以2π为最小正周期，且在区间
（
0
，
π
4
）
上单调递增的是（　　）
A．y=sin2x B．
y
=
sin
（
x
-
π
4
）
C．
y
=
cos
（
x
+
π
4
）
D．y=tan2x
组卷：475引用：4难度：0.7
解析
7．下列区间包含函数f（x）=2^x+x-4零点的为（　　）
A．（-1，0） B．（0，1） C．（1，2） D．（2，3）
组卷：237引用：3难度：0.7
解析

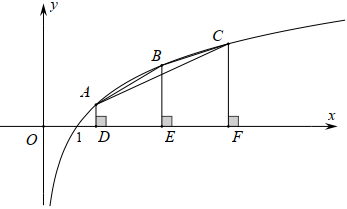20．如图，在函数f（x）=log₂x图象任取三点A（a,f（a）），B（b,f（b）），C（c,f（c）），满足a≥1，b=a+2，c=b+2，分别过A、B、C三点作x轴垂线交x轴于D、E、F．
（Ⅰ）当a=2时，求梯形ADEB的周长；
（Ⅱ）用a表示△ABC的面积S，并求S的最大值．
组卷：254引用：2难度：0.7
解析
21．已知整数m,n≥3，集合X_n={（x₁，x₂，⋯，x_n）|x_i∈{0，1}，i=1，2，⋯，n}，对于X_n中的任意两个元素A=（a₁，a₂，⋯，a_n），B=（b₁，b₂，⋯，b_n），定义A与B之间的距离为d（A，B）=
n
∑
i
=
1
|
a
i
-
b
i
|
．
若A₁，A₂，⋯，A_n∈X_n且d（A₁，A₂）=d（A₂，A₃）=⋯=d（A_m-1，A_n），则称A₁，A₂，⋯，A_m是X_n中的一个等距序列．
（Ⅰ）若A₁=（1，0，0，0），A₂=（1，1，0，0），A₃=（0，1，1，0），A₄=（0，1，1，1），判断A₁，A₂，A₃，A₄是否是X₄中的一个等距序列？
（Ⅱ）设A，B，C是X₃中的等距序列，求证：d（A，C）为偶数；
（Ⅲ）设A₁，A₂，⋯，A_m是X₆中的等距序列，且
A
1
=
（
1
，
1
，
⋯
，
1
）
6
个
1
，
A
m
=
（
0
，
0
，
⋯
，
0
）
6
个
0
，d（A₁，A₂）=5．求m的最小值．
组卷：246引用：5难度：0.4
解析