2021-2022学年北京二中高二（下）期中数学试卷

一、选择题（每小题4分，共40分）

• 1．在等比数列{a_n}中，a₁=1，a₄=-8，则{a_n}的前6项和为（　　）

  A．-21

  B．11

  C．31

  D．63
  组卷：539引用：5难度：0.9

  解析

• 2．已知二项式（2x²-

  1

  x

  ）ⁿ的所有二项式系数之和等于128，那么其展开式中含

  1

  x

  项的系数是（　　）

  A．-84

  B．-14

  C．14

  D．84
  组卷：451引用：21难度：0.7

  解析

• 3．可导函数y=f（x）在一点的导数值为0是函数y=f（x）在这点取极值的（　　）

  A．充分非必要条件	B．必要非充分条件
  C．充要条件	D．既不必要也不充分条件
  组卷：144引用：26难度：0.9

  解析

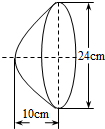• 4．如图所示，汽车前灯反光镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反光镜的轴垂直，灯泡位于抛物线的焦点处．已知灯口的直径是24cm,灯深10cm,那么灯泡与反光镜的顶点（即截得抛物线的顶点）距离为（　　）

  A．10cm

  B．7.2cm

  C．3.6cm

  D．2.4cm
  组卷：152引用：7难度：0.9

  解析

• 5．已知函数f（x）=-x³+ax²-x-1在（-∞，+∞）上是单调递减函数，则实数a的取值范围是（　　）

  A．（-∞，- 3 ）∪（ 3 ，+∞）	B．（- 3 ， 3 ）
  C．（-∞，- 3 ]∪[ 3 ，+∞）	D．[- 3 ， 3 ]
  组卷：672引用：9难度：0.8

  解析

• 6．我国古代典籍《周易》用“卦”描述万物的变化，每一卦由六爻组成．其中有一种起卦方法称为“金钱起卦法”，其做法为：取三枚相同的钱币合于双手中，上下摇动数下使钱币翻滚摩擦，再随意抛撒钱币到桌面或平盘等硬物上，如此重复六次，得到六爻．若三枚钱币全部正面向上或全部反面向上，就称为变爻．若每一枚钱币正面向上的概率为

  1

  2

  ，则一卦中恰有三个变爻的概率为（　　）

  A． 5 16

  B． 15 64

  C． 135 1024

  D． 1215 4096
  组卷：341引用：5难度：0.6

  解析

• 7．在函数f（x）=-e^x-x的图象上任意一点处的切线为l₁，若总存在函数g（x）=ax+2cosx的图象点，使得在该点处的切线1₂满足l₁⊥1₂，则a的取值范围是（　　）

  A．（-∞，-1]

  B．（2，+∞）

  C．（-1，2）

  D．[-1，2]
  组卷：321引用：6难度：0.7

  解析

三、解答题（共6小题，共85分）

• 20．设椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦点分别为F₁（-c,0），F₂（c,0），离心率为

  1

  2

  ，短轴长为

  2

  3

  ．
  （1）求椭圆C的标准方程；
  （2）设左、右顶点分别为A、B，点M在椭圆上（异于点A、B），求k_MAk_MB的值；
  （3）过点F₂作一条直线与椭圆C交于P，Q两点，过P，Q作直线

  x

  =

  a

  2

  c

  的垂线，垂足为S，T．试问：直线PT与QS是否交于定点？若是，求出该定点的坐标，否则说明理由．
  组卷：175引用：6难度：0.6

  解析

• 21．对于序列A₀：a₁，a₂，…，a_n（n∈N^*），实施变换T得序列A₁：a₁+a₂，a₂+a₃，…，a_n-1+a_n，记作A₁=T（A₀）：对A₁继续实施变换T得序列A₂=T（A₁）=T（T（A₀）），记作A₂=T₂（A₀）；…；A_n-1=T_n-1（A₀）．最后得到的序列A_n-1只有一个数，记作S（A₀）．
  （Ⅰ）若序列A₀为1，2，3，求S（A₀）；
  （Ⅱ）若序列A₀为1，2，…，n,求S（A₀）；
  （Ⅲ）若序列A和B完全一样，则称序列A与B相等，记作A=B，若序列B为序列A₀：1，2，…，n的一个排列，请问：B=A₀是S（B）=S（A₀）的什么条件？请说明理由．
  组卷：105引用：3难度：0.1

  解析