当前位置：试卷中心 > 试卷详情

2023-2024学年山东省济南市高新区八年级（上）期中数学试卷

发布：2024/10/2 15:0:2

一、选择题（本大题共10个小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．下列各数是无理数的是（　　）
A．0 B．
4
C．π D．2.
•
0
•
1
组卷：141引用：3难度：0.9
解析
2．在平面直角坐标系中，点M（-3，1）在（　　）
A．第四象限 B．第三象限 C．第二象限 D．第一象限
组卷：213引用：8难度：0.9
解析
3．下列二次根式中，属于最简二次根式的是（　　）
A．
7
B．
12
C．
8
D．
1
.
5
组卷：197引用：3难度：0.7
解析
4．下列计算正确的是（　　）
A．
2
3
-
3
=
3
B．
2
+
3
=
5
C．
3
5
×
5
=
4
5
D．
（
-
3
）
2
=
-
3
组卷：549引用：7难度：0.5
解析
5．在平面直角坐标系中，点P（1，-2）关于y轴的对称点的坐标是（　　）
A．（1，2） B．（-1，-2） C．（-1，2） D．（-2，1）
组卷：432引用：12难度：0.9
解析
6．在平面直角坐标系中，点M（4，-3）到x轴的距离为（　　）
A．4 B．3 C．-4 D．-3
组卷：550引用：7难度：0.9
解析
7．若函数y=（m-1）
x
m
2
+3是一次函数，则m的值为（　　）
A．-1 B．1 C．0 D．-1或1
组卷：1162引用：5难度：0.8
解析
8．已知（-1，y₁），（1，y₂）是直线y=-x+3上的两点，则y₁，y₂的大小关系是（　　）
A．y₁＞y₂ B．y₁＜y₂ C．y₁=y₂ D．无法确定
组卷：947引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10个小题，共86分.解答应写出文字说明、证明过程或演算步骤.）

25．（一）问题提出
（1）平面直角坐标系中，如果A、B是x轴上的点，他们对应的横坐标分别是x_A，x_B，C、D是y轴上的两点，它们对应的纵坐标分别是y_c，y_D，那么A、B两点间的距离，C、D两点间的距离分别是多少？
（2）平面直角坐标系中任意一点P（x,y）到原点的距离是多少？
（3）已知平面上的两点P₁（x₁，y₁），P₂（x₂，y₂），如何求P₁，P₂的距离|P₁P₂|．
（二）问题探究
（1）求平面直角坐标系中x轴上的两点E（5，0）、F（-2，0）之间的距离，可以借助绝对值表示|EF|=|5-（-2）|=7，对于y轴上两点，M（0，-3）、N（0，5）之间的距离|MN|=|3-5|=2．
结论：在平面直角坐标系中，如果A、B是x轴上两点，它们对应的横坐标分别是x_A，x_B，则A、B两点间的距离|AB|=
；C、D是y轴上的两点，它们对应的纵坐标分别是y_c，y_D，那么C、D两点间的距离|CD|=
．
（2）如图1：平面直角坐标系中任意一点B（3，4），过B向x轴上作垂线，垂足为M，由勾股定理得|OB|=
；结论：平面直角坐标系中任意一点P（x,y）到原点的距离|OP|=
；
（3）如图2，要求AB或DE的长度，可以转化为求Rt△ABC或Rt△DEF的斜边长，例如：从坐标系中发现：D（-7，5），E（4，-3）所以|DF|=|5-（-3）|=8，|EF|=|4-（-7）|=11，所以由勾股定理得：|DE|=
8
2
+
1
1
2
=
185
．在图2中请用上面的方法求线段AB的长：AB=
；在图3中：设P₁（x₁，y₁），P₂（x₂，y₂），试用x₁，x₂，y₁，y₂表示：|P₁P₂|=
．
（三）拓展应用
试用以上所得结论解决如下问题：已知A（0，1），B（4，3）．
（1）直线AB与x轴交于点D，求线段BD的长．
（2）C为坐标轴上的点，且使得△ABC是以AB为底边的等腰三角形，则C的坐标为
（不必写出解答过程，直接写出即可）．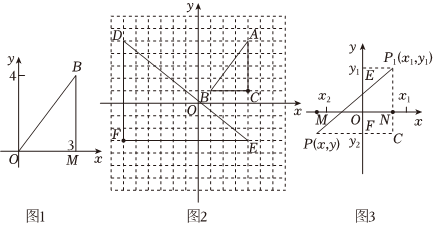
组卷：239引用：1难度：0.5
解析
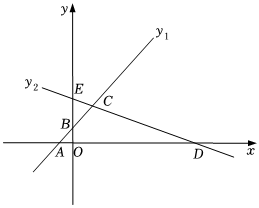26．如图，在平面直角坐标系中，一次函数y₁=x+2的图象与x轴，y轴分别交于点A，B，
y
2
=
-
1
3
x
+
b
的图象与x轴，y轴分别交于点D，E，且两个函数图象相交于点C（m,5）．
（1）填空：m=
，b=
；
（2）求△ACD的面积；
（3）在线段AD上是否存在一点M，使得△ABM的面积与四边形BMDC的面积比为4：21？若存在，请求出点M的坐标；若不存在，请说明理由．
（4）点P在线段AD上，连接CP，若△ACP是直角三角形，请直接写出所有符合条件的点P坐标．
组卷：3140引用：7难度：0.3
解析