当前位置：试卷中心 > 试卷详情

2023年江苏省扬州市仪征市中考数学模拟试卷（6月份）

发布：2024/5/25 8:0:9

一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）

1．2023的倒数是（　　）
A．2023 B．-2023 C．
-
1
2023
D．
1
2023
组卷：1957引用：72难度：0.8
解析
2．下面用数学家名字命名的图形中，既是轴对称图形又是中心对称图形的是（　　）
A．
赵爽弦图 B．
科克曲线
C．
斐波那契螺旋 D．
笛卡尔心形线
组卷：171引用：9难度：0.9
解析
3．下列运算正确的是（　　）
A．x²•x³=x⁵ B．4x²+x²=5x⁴ C．（x³）²=x⁹ D．x⁶÷x²=x³
组卷：16引用：1难度：0.8
解析
4．为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如表所示：

月用水量（吨） 3 4 5 6

户数 4 6 8 2

关于这若干户家庭的该月用水量的数据统计分析，下列说法正确的（　　）
A．方差是1 B．平均数是4.5
C．中位数是5 D．众数是5
组卷：134引用：4难度：0.7
解析
5．我国古代数学名著《九章算术》中记载：“粟米之法：粟率五十；粝米三十．今有米在十斗桶中，不知其数．满中添粟而舂之，得米七斗．问故米几何？”意思为：50斗谷子能出30斗米，即出米率为
3
5
．今有米在容量为10斗的桶中，但不知道数量是多少．再向桶中加满谷子，再舂成米，共得米7斗．问原来有米多少斗？如果设原来有米x斗，向桶中加谷子y斗，那么可列方程组为（　　）
A．
x
+
y
=
10
x
+
3
5
y
=
7
B．
x
+
y
=
10
3
5
x
+
y
=
7
C．
x
+
y
=
7
x
+
5
3
y
=
10
D．
x
+
y
=
7
5
3
x
+
y
=
10
组卷：2139引用：28难度：0.7
解析
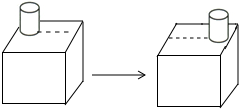6．如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（　　）
A．主视图 B．左视图
C．俯视图 D．主视图和俯视图
组卷：339引用：12难度：0.8
解析
7．如图，平行四边形OABC的周长为7，∠AOC=60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数
y
=
k
x
（
x
＞
0
）
的图象经过OABC顶点A和BC的中点M，则k的值为（　　）
A．
3
B．
2
3
C．
3
3
D．
4
3
组卷：232引用：2难度：0.5
解析
8．如图，点A坐标为（-2，1），点B坐标为（0，4），将线段AB绕点O按顺时针方向旋转得到对应线段A′B′，若点A′恰好落在x轴上，则∠B'A′O的正弦值为（　　）
A．
8
5
5
B．
2
5
5
C．
1
65
65
D．
8
65
65
组卷：231引用：4难度：0.7
解析

二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

9．清代•袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为
．
组卷：663引用：24难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

27．华罗庚是我国著名的数学家，他推广的优选法，就是以黄金分割法为指导，用最可能少的试验次数，尽快找到生产和科学实验中最优方案的一种科学试验方法．黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，这个比例被公认为最能引起美感的比例，因此被称为黄金分割．如图1，点B把线段AC分成两部分，如果
BC
AB
=
AB
AC
，那么称B为线段AC的黄金分割点，它们的比值为
5
-
1
2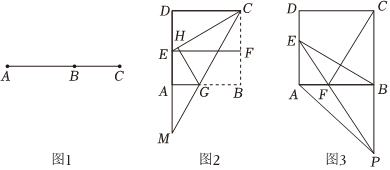
．

（1）如图1，若BC=3，则AB的长为
；
（2）如图2，用边长为20cm的正方形纸片进行如下操作：对折正方形ABCD得到折痕EF，连接CE，将CB折叠到CE上，点B对应点为点H，折痕为CG．延长CG交DA的延长线于点M．求证：A是DM的黄金分割点；
（3）如图3，在正方形ABCD的边AD上任取一点E（AE＞DE），连接BE，作CF⊥BE，交AB于点F，延长EF交CB的延长线交于点P，连接AP．若F为AB的黄金分割点，求cos∠BAP的值．
组卷：214引用：2难度：0.3
解析
28．如图，二次函数y=ax²+bx+c的图象经过点A（1，0），B（3，0）与y轴正半轴交于点C，连接AC，tan∠OAC=3．△DFE的顶点E，F在x轴上，∠DFE=90°，DF=EF=2，点F（-2，0）．将△DFE沿x轴向右平移，平移距离为m（m＞0）．
（1）求二次函数的表达式；
（2）△DFE向右移动过程中，是否存在点E使得△ACE是等腰三角形，若存在，请求出m的值．若不存在请说明理由；
（3）①当点D首次落在抛物线上，求m的值．
②当抛物线落在△DFE内的部分，满足y随x的增大而减小时，请直接写出m的取值范围．
组卷：593引用：3难度：0.3
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．赵爽弦图	B．科克曲线
C．斐波那契螺旋	D．笛卡尔心形线

A．方差是1	B．平均数是4.5
C．中位数是5	D．众数是5

A．主视图	B．左视图
C．俯视图	D．主视图和俯视图

月用水量（吨）	3	4	5	6
户数	4	6	8	2

2023年江苏省扬州市仪征市中考数学模拟试卷（6月份）

一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）

1．2023的倒数是（ ）

2．下面用数学家名字命名的图形中，既是轴对称图形又是中心对称图形的是（ ）

3．下列运算正确的是（ ）

4．为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如表所示： 月用水量（吨） 3 4 5 6 户数 4 6 8 2 关于这若干户家庭的该月用水量的数据统计分析，下列说法正确的（ ）

6．如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（ ）

7．如图，平行四边形OABC的周长为7，∠AOC=60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数y=kx（x＞0）的图象经过OABC顶点A和BC的中点M，则k的值为（ ）

8．如图，​点A坐标为（-2，1），点B坐标为（0，4），将线段AB绕点O按顺时针方向旋转得到对应线段A′B′，若点A′恰好落在x轴上，则∠B'A′O的正弦值为（ ）

二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）

9．清代•袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为 ．

三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

1．2023的倒数是（　　）

2．下面用数学家名字命名的图形中，既是轴对称图形又是中心对称图形的是（　　）

3．下列运算正确的是（　　）

4．为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如表所示：

月用水量（吨） 3 4 5 6

户数 4 6 8 2

关于这若干户家庭的该月用水量的数据统计分析，下列说法正确的（　　）

6．如图，一个圆柱体在正方体上沿虚线从左向右平移，平移过程中不变的是（　　）

7．如图，平行四边形OABC的周长为7，∠AOC=60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数
y
=
k
x
（
x
＞
0
）
的图象经过OABC顶点A和BC的中点M，则k的值为（　　）

8．如图，点A坐标为（-2，1），点B坐标为（0，4），将线段AB绕点O按顺时针方向旋转得到对应线段A′B′，若点A′恰好落在x轴上，则∠B'A′O的正弦值为（　　）

9．清代•袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来．苔花如米小，也学牡丹开．”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为
．