2023年湖北省襄阳市宜城市中考数学适应性试卷
发布:2024/5/18 8:0:8
一、选择题:(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将其标号在答题卡上涂黑作答.)
-
1.-3的绝对值的相反数是( )
组卷:209引用:26难度:0.9 -
2.下列图形:等边三角形,等腰梯形,正方形,圆中,既是轴对称图形又是中心对称图形的有( )
组卷:42引用:1难度:0.9 -
3.下列计算正确的是( )
组卷:166引用:4难度:0.8 -
 4.如图所示几何体的左视图是( )组卷:45引用:3难度:0.8
4.如图所示几何体的左视图是( )组卷:45引用:3难度:0.8 -
5.已知反比例函数y=-
,当1<x<3时,y的取值范围是( )6x组卷:92引用:1难度:0.5 -
6.下列事件中,是必然事件的是( )
组卷:22引用:1难度:0.8 -
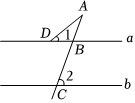 7.如图,直线a∥b,∠1=39°,∠2=70°,则∠A度数是( )组卷:41引用:2难度:0.6
7.如图,直线a∥b,∠1=39°,∠2=70°,则∠A度数是( )组卷:41引用:2难度:0.6 -
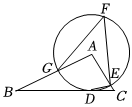 8.如图,在△ABC中,∠B=30°,以点A为圆心的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠GFE=50°,则∠CDE的度数是( )组卷:126引用:2难度:0.7
8.如图,在△ABC中,∠B=30°,以点A为圆心的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠GFE=50°,则∠CDE的度数是( )组卷:126引用:2难度:0.7
三、解答题(本大题共9个小题,共72分.解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.)
-
24.已知菱形ABCD的边长为4.∠ADC=60°,等边△AEF两边分别交边DC,CB于点E,F.
(1)特殊发现:如图1,若点E,F分别是边DC,CB的中点.求证:菱形ABCD对角线AC,BD的交点O即为等边△AEF的外心;
(2)若点E,F始终分别在边DC,CB上移动,等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪条直线上,并加以证明;
②学以致用:如图3,当△AEF的面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,求的值.1DM+1DN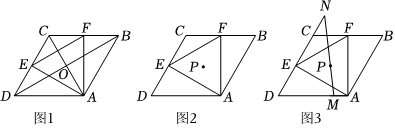 组卷:53引用:1难度:0.3
组卷:53引用:1难度:0.3 -
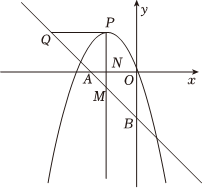 25.如图,在平面直角坐标系中,直线y=-x-2与x轴交于点A,与y轴交于点B,抛物线y=-(x-m)2+m2的顶点为P,过点P分别作x轴,y轴的垂线交AB于点M,Q,直线PM交x轴于点N.
25.如图,在平面直角坐标系中,直线y=-x-2与x轴交于点A,与y轴交于点B,抛物线y=-(x-m)2+m2的顶点为P,过点P分别作x轴,y轴的垂线交AB于点M,Q,直线PM交x轴于点N.
(1)若点P在y轴的左侧,且N为PM中点,求抛物线的解析式;
(2)求线段PQ长的最小值,并求出当PQ的长度最小时点P的坐标;
(3)若P,M,N三点中,任意两点都不重合,且PN>MN,求m的取值范围.组卷:126引用:3难度:0.3


