2023-2024学年吉林省长春市博硕学校高三（上）期初数学试卷

一、单选题（本题共8小题，每小题5分，共40分．）

• 1．已知集合M={-1，1}，下列选项正确的是（　　）

  A．{-1}∈M

  B．∅∈M

  C．-1⊆M

  D．{-1}⊆M
  组卷：99引用：3难度：0.8

  解析

• 2．2^x＞2是x²＞1的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：2引用：2难度：0.6

  解析

• 3．某市一次高三模拟考试一共有3.2万名考生参加，他们的总分ξ服从正态分布N（480，σ²），若P（430≤ξ≤530）=0.78，则总分高于530分的考生人数为（　　）

  A．2400

  B．3520

  C．8520

  D．12480
  组卷：311引用：7难度：0.8

  解析

• 4．已知

  C

  0

  n

  +

  2

  C

  1

  n

  +

  2

  2

  C

  2

  n

  +

  2

  3

  C

  3

  n

  +

  ⋯

  +

  2

  n

  C

  n

  n

  =

  81

  ，则

  C

  1

  n

  +

  C

  2

  n

  +

  C

  3

  n

  +

  ⋯

  +

  C

  n

  n

  等于（　　）

  A．15

  B．16

  C．7

  D．8
  组卷：422引用：6难度：0.8

  解析

• 5．在射击比赛中，甲乙两人对同一目标各进行一次射击，甲击中目标的概率为

  3

  5

  ，乙击中目标的概率为

  4

  5

  ，在目标被击中的情况下，甲击中目标的概率为（　　）

  A． 3 4

  B． 12 25

  C． 15 23

  D． 3 7
  组卷：776引用：4难度：0.8

  解析

• 6．设某医院仓库中有10盒同样规格的X光片，已知其中有5盒、3盒、2盒依次是甲厂、乙厂、丙厂生产的．且甲、乙、丙三厂生产该种X光片的次品率依次为

  1

  10

  ，

  1

  15

  ，

  1

  20

  ，现从这10盒中任取一盒，再从这盒中任取一张X光片，则取得的X光片是次品的概率为（　　）

  A．0.08

  B．0.1

  C．0.15

  D．0.2
  组卷：2332引用：18难度：0.7

  解析

四、解答题（本题共4小题，共50分，解答应写出文字说明、证明过程或者演算步骤）

• 17．某品牌中性笔研发部门从流水线上随机抽取100件产品，统计其性能指数并绘制频率分布直方图（如图1）
  
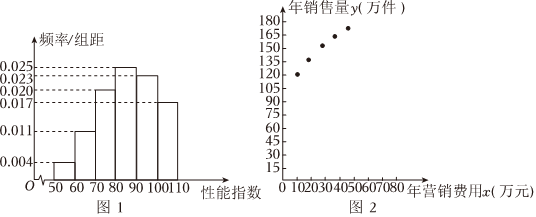
  产品的性能指数在[50，70）的适合儿童使用（简称A类产品），在[70，90）的适合少年使用（简称B类产品），在[90，110]的适合青年使用（简称C类产品），A，B，C三类产品的销售利润分别为每件1.5，3.5，5.5（单位：元）．以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率．
  （1）该公司为了解年营销费用x（单位：万元）对年销售量y（单位：万件）的影响，对近5年的年营销费用x_i和年销售量y_i（i=1，2，3，4，5）的数据做了初步处理，得到散点图（如图2）及一些统计量的值（如下表）．
  

  5 ∑ i = 1 u i	5 ∑ i = 1 v i	5 ∑ i = 1 （ u i - u ） （ v i - v ）	5 ∑ i = 1 （ u i - u ） 2
  16.30	24.87	0.41	1.64

  表中

  u

  i

  =

  ln

  x

  i

  ，

  v

  i

  =

  ln

  y

  i

  ，

  u

  =

  1

  5

  5

  ∑

  i

  =

  1

  u

  i

  ，

  v

  =

  1

  5

  5

  ∑

  i

  =

  1

  v

  i

  ．
  根据散点图判断，y=a•x^b可以作为年销售量y（万件）关于年营销费用x（万元）的回归方程，求y关于x的回归方程；（取e^4.159=64）
  （2）求每件产品的平均销售利润；并用所求的回归方程估计该公司应投入多少营销费，才能使得该产品一年的收益达到最大？（收益=销售利润-营销费用）
  参考公式：对于一组数据（u₁，v₁），（u₂，v₂），⋯，（u_n，v_n），其回归直线

  ̂

  v

  =

  ̂

  α

  +

  ̂

  β

  u

  的斜率和截距的最小二乘估计分别为

  ̂

  β

  =

  n

  ∑

  i

  =

  1

  （

  u

  i

  -

  u

  ）

  （

  v

  i

  -

  v

  ）

  n

  ∑

  i

  =

  1

  （

  u

  i

  -

  u

  ）

  2

  ，

  ̂

  α

  =

  v

  -

  ̂

  β

  u

  ．
  组卷：57引用：2难度：0.4

  解析

• 18．（1）证明：当x＜1时，x+1≤e^x≤

  1

  1

  -

  x

  ；
  （2）是否存在正数a,使得f（x）=2e^x+asinx-ax²-（a+2）x在R上单调递增，若存在，求出a的取值范围；若不存在，请说明理由．
  组卷：34引用：3难度：0.5

  解析