2020-2021学年浙江省温州市永嘉县岩头中学九年级（上）月考数学试卷（12月份）

一、选择题（共十题：共40分）

• 1．已知⊙O的半径为5，点P在⊙O内，则OP的长可能是（　　）

  A．7

  B．6

  C．5

  D．4
  组卷：2160引用：35难度：0.9

  解析

• 2．抛物线y=（x-3）²+1的对称轴为直线（　　）

  A．x=1

  B．x=-1

  C．x=3

  D．x=-3
  组卷：9引用：2难度：0.6

  解析

• 3．在一个不透明的口袋里装有2个白球和4个红球，它们除颜色外其余都相同，现随机从袋里摸出1个球，则摸出白球的概率是（　　）

  A． 1 2

  B． 1 3

  C． 2 3

  D． 3 4
  组卷：83引用：2难度：0.7

  解析

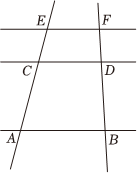• 4．如图，AB∥CD∥EF，若

  CE

  AC

  =

  1

  2

  ，则下列论断中，错误的是（　　）

  A． CE AE = 1 3

  B． AC AE = 2 3

  C． DF BD = 1 2

  D． CD AB = 1 2
  组卷：8引用：1难度：0.5

  解析

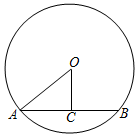• 5．如图，在⊙O中，弦AB=8，OA=5，则弦心距OC的长是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：105引用：2难度：0.6

  解析

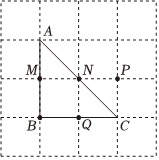• 6．如图，在4×4的网格中，A，B，C是三个格点，其中每个小正方形的边长均为1，则△ABC的外心可能是（　　）

  A．点M

  B．点N

  C．点P

  D．点Q
  组卷：26引用：1难度：0.5

  解析

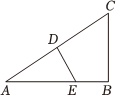• 7．如图，在Rt△ABC中，D是斜边AC的中点，DE⊥AC交AB于点E，若AB=6，BC=4，则DE的长为（　　）

  A．2

  B． 13 3

  C． 2 13 3

  D．3
  组卷：7引用：1难度：0.6

  解析

• 8．已知点A（-2，a），B（-1，b），C（2，c）是抛物线y=-mx²+2mx+4（m＞0）上的三点，则a,b,c的大小关系为（　　）

  A．c＞a＞b

  B．c＞b＞a

  C．b＞a＞c

  D．b＞c＞a
  组卷：12引用：1难度：0.6

  解析

三、解答题（共八题：共80分）

• 23．某商店销售一种商品A，每件进价为9元．经市场调查表明，当售价在10到14元之间（含10元，14元）浮动时，每件售价每增加0.5元时，日均销售量减少40件；当售价为12元时，日均销售量为400件．设每件售价为x元（10≤x≤14），每天销售量为y件
  （1）求y关于x的函数表达式；
  （2）设该商店销售商品A每日获得利润W元，当售价为多少元时，每日可获得最大利润？最大利润是多少？
  （3）为促进公益，该商店决定从每日销售商品A的利润中捐赠m元（m为正整数）给慈善机构，且捐赠后销售商品A的利润不低于1200元，求m的最大值．
  组卷：19引用：1难度：0.7

  解析

• 24．如图，在矩形ABCD中，AB=6，AD=8，P是AD边上一点，以BP为直径的⊙O交AC于点E，连结BP交AC于点G．
  
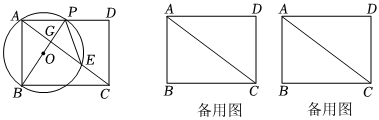
  （1）若P是AD中点时，求BP和PE的长；
  （2）若P，E分别在射线AD，射线AC上移动，当△PEG是等腰三角形时，求AP的长；
  （3）若⊙O交BC边于点F，连结PF，作点O关于PF的对称点O'，当O'落在△ACD内部时（不含边界），请直接写出AP的取值范围．
  组卷：14引用：1难度：0.5

  解析