当前位置：试卷中心 > 试卷详情

2023-2024学年湖北省部分学校高三（上）起点数学试卷（8月份）

发布：2024/8/3 8:0:9

1．已知集合A={x|x²-x-2≥0}，B={-2，-1，0，1}，则A∩B=（　　）
A．{-2，-1，0} B．{-1，0，1} C．{-2} D．{-2，-1}
组卷：263引用：7难度：0.7
解析
2．已知
z
=
2
1
-
i
+
i
，则
z
-
z
=（　　）
A．-4i B．4i C．2 D．-2
组卷：119引用：6难度：0.8
解析
3．设a,b是实数，则“a＞|b|”是“ln（a²+1）＞ln（b²+1）”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：163引用：7难度：0.7
解析
4．已知椭圆
C
：
x
2
a
2
+
y
2
9
=
1
（
a
＞
3
）
的离心率为
3
2
，则a=（　　）
A．5 B．6 C．7 D．8
组卷：242引用：4难度：0.8
解析
5．已知锐角α满足
tanα
=
2
2
，则sin2α=（　　）
A．
2
2
3
B．
2
3
C．
2
3
D．
1
3
组卷：430引用：7难度：0.7
解析
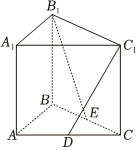6．在直三棱柱ABC-A₁B₁C₁中，AB⊥BC，AB=BC=AA₁，D，E分别为AC，BC的中点，则异面直线C₁D与B₁E所成角的余弦值为（　　）
A．
3
3
B．
5
5
C．
10
10
D．
30
10
组卷：638引用：11难度：0.5
解析
7．在△ABC中，点M在线段BC上，
AN
=
2
3
AM
=
λ
AB
+
μ
AC
，则λ+μ=（　　）
A．
1
4
B．
1
3
C．
2
3
D．1
组卷：215引用：4难度：0.8
解析

21．已知抛物线C：y²=2px（p＞0）的焦点为F，过F作斜率为k（k＞0）的直线l与C交于A，B两点，当
k
=
2
时，|AB|=6．
（1）求抛物线C的标准方程；
（2）设线段AB的中垂线与x轴交于点P，抛物线C在A，B两点处的切线相交于点Q，设P，Q两点到直线l的距离分别为d₁，d₂，求
d
1
d
2
的值．
组卷：108引用：4难度：0.5
解析
22．已知函数f（x）=a（e^x-1）-x²+x.
（1）当a=1时，求f（x）的图象在点（0，f（0））处的切线方程；
（2）若a⩾1，证明：当x＞0时，f（x）+cosx＞1．
组卷：177引用：5难度：0.5
解析