2023-2024学年湖南省株洲二中教育集团高三（上）开学联考数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|x²≤1}，B={x|x²-2x-3＜0}，则A∩B=（　　）

  A．（-1，1]

  B．[-1，1]

  C．（-1，3）

  D．[-1，3）
  组卷：113引用：3难度：0.9

  解析

• 2．若复数z满足z（2-i）=1+4i（i是虚数单位），则复数z的共轭复数为（　　）

  A．- 2 5 + 9 5 i

  B．- 2 5 - 9 5 i

  C． 2 5 + 9 5 i

  D． 2 5 - 9 5 i
  组卷：695引用：4难度：0.9

  解析

• 3．已知平面向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  |

  b

  |

  =

  1

  ，

  a

  ，

  b

  的夹角为60°，

  |

  a

  +

  t

  b

  |

  =

  3

  （

  t

  ∈

  R

  ）

  ，则实数t=（　　）

  A．±1

  B．1

  C．-1

  D． 1 2
  组卷：39引用：4难度：0.7

  解析

• 4．已知正实数m,n,满足m+n=1，则下列不等式中错误的是（　　）

  A． mn ≤ 1 4

  B．2m2+2n2≥1

  C． 1 m + 2 n ≥ 3 + 2 2

  D． m + n ≤ 1
  组卷：385引用：3难度：0.5

  解析

• 5．已知等差数列{a_n}的公差为d,数列{b_n}满足

  a

  n

  •

  b

  n

  =

  1

  （

  n

  ∈

  N

  *

  ）

  ，则“d＞0”是“{b_n}为递减数列”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：310引用：6难度：0.7

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  lo

  g

  1

  3

  （

  3

  x

  2

  -

  ax

  +

  8

  ）

  在[-1，+∞）上单调递减，则实数a的取值范围是（　　）

  A．（-∞，-6]

  B．[-11，-6]

  C．（-11，-6]

  D．（-11，+∞）
  组卷：234引用：7难度：0.6

  解析

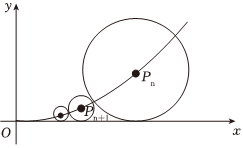• 7．如图，在xOy平面上有一系列点P₁（x₁，y₁），P₂（x₂，y₂），…，P_n（x_n，y_n）…，对每个正整数n,点P_n位于函数y=x²（x≥0）的图像上，以点P_n为圆心的⊙P_n都与x轴相切，且⊙P_n与⊙P_n+1外切．若x₁=1，且x_n+1＜x_n（n∈N*），T_n=x_nx_n+1，{T_n}的前n项之和为S_n，则S₂₀=（　　）

  A． 39 40

  B． 40 41

  C． 80 41

  D． 20 41
  组卷：54引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知F是椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左焦点，O为坐标原点，M为椭圆上任意一点，椭圆的离心率为

  3

  2

  ，△MOF的面积的最大值为

  3

  2

  ．
  （1）求椭圆C的方程；
  （2）A，B为椭圆的左，右顶点，点P（1，0），当M不与A，B重合时，射线MP交椭圆C于点N，直线AM，BN交于点T，求∠ATB的最大值．
  组卷：151引用：5难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  2

  x

  2

  -

  x

  -

  1

  ，
  （1）证明：当x＞0时，f（x）＞0恒成立；
  （2）若关于x的方程

  f

  （

  x

  ）

  x

  +

  x

  2

  =

  asinx

  在（0，π）内有解，求实数a的取值范围．
  组卷：36引用：3难度：0.3

  解析