当前位置：试卷中心 > 试卷详情

2022-2023学年甘肃省兰州市安宁区东方中学八年级（上）期中数学试卷

发布：2024/9/25 10:0:2

1．下列实数是无理数的是（　　）
A．-2 B．0 C．-
1
2
D．
3
组卷：115引用：10难度：0.9
解析
2．下列计算正确的是（　　）
A．
（
-
3
）
2
=-3 B．
12
÷
3
=2 C．
4
1
9
=2
1
3
D．
（
-
2
5
）
2
=10
组卷：556引用：8难度：0.9
解析
3．若x,y为实数，且
|
x
+
2
|
+
y
-
2
=
0
，则
（
y
x
）
2021
的值为（　　）
A．1 B．-1 C．2 D．-2
组卷：171引用：4难度：0.7
解析
4．若点P的坐标为（2022，-1），则点P在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：170引用：5难度：0.7
解析
5．若点A（1+m,1-n）与点B（-3，2）关于y轴对称，则m-n的值是（　　）
A．-1 B．-3 C．1 D．3
组卷：600引用：5难度：0.8
解析
6．如图，将北京市地铁部分线路图置于正方形网格中，若崇文门站的坐标为（0，-1），西单站的坐标为（-5，0），则雍和宫站的坐标为（　　）
A．（4，0） B．（-4，0） C．（0，-4） D．（0，4）
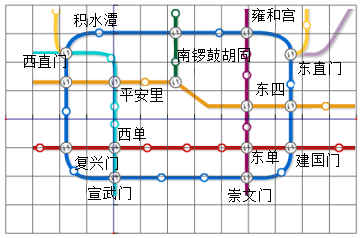组卷：208引用：2难度：0.7
解析
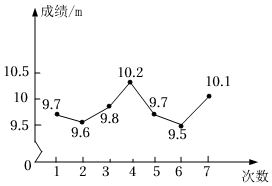7．在学校的体育训练中，小明投掷实心球的7次成绩如图所示，则这7次成绩的平均数和中位数分别是（　　）
A．9.7m,9.9m B．9.7m,9.8m C．9.8m,9.7m D．9.8m,9.9m
组卷：118引用：4难度：0.8
解析

8．下列命题中，不正确的是（　　）

A．各有一个角为100°，且底边相等的两个等腰三角形全等

B．各有一个角为36°，且底边相等的两个等腰三角形全等

C．各有一个角为50°，且其所对的直角边相等的两个直角三角形全等

D．各有一个角为40°，且有斜边相等的两个直角三角形全等

组卷：29引用：2难度：0.7

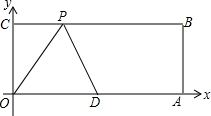27．如图，O为坐标原点，四边形OABC为长方形，边OA和OC分别落在x轴和y轴的正半轴上，且A（10，0），C（0，4），点D是OA的中点，点P在线段BC上运动，当△ODP为腰长为5的等腰三角形时，求点P的坐标．
组卷：673引用：3难度：0.3
解析
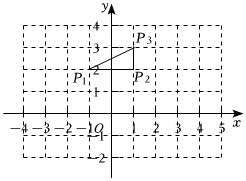28．定义：在平面直角坐标系xOy中，已知点P₁（a,b），P₂（c,b），P₃（c,d），这三个点中任意两点间的距离的最小值称为点P₁，P₂，P₃的“最佳间距”．例如：如图，点P₁（-1，2），P₂（1，2），P₃（1，3）的“最佳间距”是1．
（1）理解：点Q₁（2，1），Q₂（5，1），Q₃（5，5）的“最佳间距”是
；
（2）探究：已知点O（0，0），A（-4，0），B（-4，y）（y≠0）．
①若点O，A，B的“最佳间距”是2，则y的值为
；
②点O，A，B的“最佳间距”最大是多少？请说明理由．
（3）迁移：当点O（0，0），E（m,0），P（m,-2m+1）的“最佳间距”取到最大值时，点P的坐标是
．
组卷：59引用：1难度：0.5
解析