2022-2023学年重庆市育才中学高一（下）期末数学试卷

一、单项选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合要求的）

• 1．复数（1-3i）（1-i）的虚部为（　　）

  A．-4

  B．-4i

  C．2

  D．2i
  组卷：97引用：3难度：0.8

  解析

• 2．已知正三棱锥P-ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={Q∈S|PQ≤5}，则T表示的区域的面积为（　　）

  A． 3 π 4

  B．π

  C．2π

  D．3π
  组卷：2312引用：8难度：0.8

  解析

• 3．若直线

  x

  a

  +

  y

  b

  =1通过点M（cosα，sinα），则（　　）

  A．a2+b2≤1

  B．a2+b2≥1

  C． 1 a 2 + 1 b 2 ≤1

  D． 1 a 2 + 1 b 2 ≥1
  组卷：443引用：48难度：0.7

  解析

• 4．已知函数f（x）=sin²

  ωx

  2

  +

  1

  2

  sinωx-

  1

  2

  （ω＞0），x∈R，若f（x）在区间（π，2π）内没有零点，则ω的取值范围是（　　）

  A．（0， 1 8 ]	B．（0， 1 4 ]∪[ 5 8 ，1）
  C．（0， 5 8 ]	D．（0， 1 8 ]∪[ 1 4 ， 5 8 ]
  组卷：4821引用：36难度：0.7

  解析

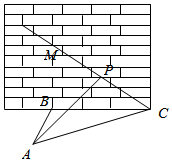• 5．如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小（仰角θ为直线AP与平面ABC所成的角）．若AB=15m,AC=25m,∠BCM=30°，则tanθ的最大值是（　　）

  A． 30 5

  B． 30 10

  C． 4 3 9

  D． 5 3 9
  组卷：2666引用：28难度：0.5

  解析

• 6．直线x+y+2=0分别与x轴，y轴交于A，B两点，点P在圆（x-2）²+y²=2上，则△ABP面积的取值范围是（　　）

  A．[2，6]

  B．[4，8]

  C．[ 2 ，3 2 ]

  D．[2 2 ，3 2 ]
  组卷：11341引用：92难度：0.5

  解析

• 7．已知α，β，γ是互不相同的锐角，则在sinαcosβ，sinβcosγ，sinγcosα三个值中，大于

  1

  2

  的个数的最大值是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：2423引用：10难度：0.4

  解析

四、解答题（本大题共70分，解答应写出必要的文字说明，证明过程或演算步骤）

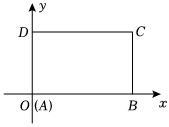• 21．在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如图所示）．将矩形折叠，使A点落在线段DC上．
  （Ⅰ）若折痕所在直线的斜率为k,试写出折痕所在直线的方程；
  （Ⅱ）求折痕的长的最大值．
  组卷：789引用：7难度：0.5

  解析

• 22．圆O：x²+y²=1，A（0，1），P（-1，1），过P直线l交圆O于B，C两点．
  （1）记三角形ABP与三角形ABC的面积分别为S₁与S₂，求

  S

  1

  S

  2

  +

  S

  2

  S

  1

  的取值范围；
  （2）若直线AB，AC分别交x轴于M，N两点，|MN|=4，求直线l的方程．
  组卷：84引用：1难度：0.5

  解析