2022-2023学年安徽省滁州市高二(下)期末数学试卷
发布:2024/6/17 8:0:9
一、单选题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.在等比数列{an}中,已知a1=1,a2=3,则a4=( )
组卷:164引用:4难度:0.7 -
2.已知函数f(x)的导函数f'(x)的图象如图所示,则f(x)的极小值点为( )
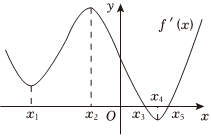 组卷:66引用:7难度:0.7
组卷:66引用:7难度:0.7 -
3.在四面体A-BCD中,E是AD的中点,F是BC的中点.设
,AB=a,AC=b,则AD=c=( )EF组卷:251引用:2难度:0.8 -
4.若函数f(x)=
-f'(1)lnx,则f'(1)=( )x组卷:42引用:1难度:0.8 -
5.抛物线y2=2x的焦点为F,点A(1,1),P为抛物线上的动点,则|PA|+|PF|的最小值为( )
组卷:270引用:3难度:0.8 -
6.甲、乙两人向同一目标各射击1次,已知甲命中目标的概率为0.7,乙命中目标的概率为0.8.在目标被击中的情况下,甲、乙同时击中目标的概率为( )
组卷:25引用:2难度:0.8 -
7.已知
存在唯一极小值点,则a的范围是( )f(x)=aexx+lnx-x组卷:67引用:1难度:0.6
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
 21.如图,已知平行四边形ABCD与椭圆相切,且A(4,1),B(-1,1),C(-4,-1),D(1,-1).x2a2+y2b2=1(a>b>0)
21.如图,已知平行四边形ABCD与椭圆相切,且A(4,1),B(-1,1),C(-4,-1),D(1,-1).x2a2+y2b2=1(a>b>0)
(1)求椭圆的方程;
(2)若点P是椭圆上位于第一象限一动点,且点P处的切线与AB,AD分别交于点E,F.证明:|BE||DF|为定值.组卷:30引用:1难度:0.5 -
22.已知f(x)=ex-a(lnx+ex),x∈(0,1].
(1)当a=1时,求f(x)在x=1处的切线方程;
(2)若f(x)≥0恒成立,且存在m>0使得方程f(x)=m恒有两个交点,求a的范围.组卷:18引用:1难度:0.6


