当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市巴南区育才实验中学七年级（下）诊断数学试卷（三）

发布：2024/7/11 8:0:9

一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧所对应的方框涂黑．

1．下列各数中，无理数是（　　）
A．0.
•
5
B．
π
2
C．
22
3
D．3.121121121112
组卷：217引用：7难度：0.9
解析
2．图中，∠1和∠2不是同位角的是（　　）
A． B． C． D．
组卷：552引用：2难度：0.7
解析
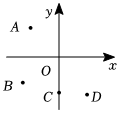3．若一个点的坐标为（-2，3），则这个点在如图所示的平面直角坐标系上的位置可能是（　　）
A．点A B．点B C．点C D．点D
组卷：64引用：2难度：0.8
解析
4．若二次根式
1
-
x
有意义，则实数x的取值范围是（　　）
A．x≠1 B．x≤1 C．x≥1 D．x＞0且x≠1
组卷：240引用：4难度：0.5
解析
5．估算
13
-
3
的值，下列结论正确的是（　　）
A．0和1之间 B．1和2之间 C．2和3之间 D．3和4之间
组卷：523引用：4难度：0.7
解析
6．下列命题中，真命题的是（　　）
A．垂直于同一条直线的两条直线互相平行
B．互补的角是邻补角
C．内错角相等
D．平移前后图形的形状和大小都没有发生改变
组卷：73引用：3难度：0.5
解析
7．把一副三角板按如图所示平放在桌面上，点E恰好落在CB的延长线上，FE⊥CE，则∠ADE的大小为（　　）
A．165° B．155° C．145° D．135°
组卷：1061引用：6难度：0.5
解析
8．《九章算术》是我国东汉初年编订的一部数学经典著作，在它的“方程”里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排的，如图1、图2图中各行从左到右列出的算筹分别表示未知数x,y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是
3
x
+
2
y
=
19
x
+
4
y
=
23
，类似地，图2所示的算筹图我们可以表述为（　　）
A．
2
x
+
y
=
11
4
x
+
3
y
=
27
B．
2
x
+
y
=
11
4
x
+
3
y
=
22
C．
3
x
+
2
y
=
19
x
+
4
y
=
23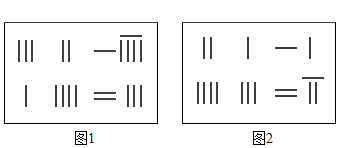
D．
2
x
+
y
=
6
4
x
+
3
y
=
27
组卷：430引用：16难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（本大题8个小题，19题、20题各8分，21题、22题、23题、24题、25题各10分，26题12分）

25．阅读下列材料，回答问题．
对任意一个三位数n,如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，因为666÷111=6，所以F（123）=6．
（1）计算：F（341）=
，F（625）=
；
（2）若s,t都是“相异数”，其中s=100x+32，t=150+y,1≤x≤9，1≤y≤9且x,y都是正整数，规定k=F（s）-F（t），当F（s）+F（t）=19时，求k的最小值．
组卷：537引用：2难度：0.3
解析
26．已知：如图，直线a∥b,AC⊥BC于点C，连结AB且分别交直线a、b于点E、F．
（1）如图1，若∠DEF和∠EFG的角平分线EM、FM交于点M，请求∠M的度数；
（2）如图2，若∠EDC的角平分线DM分别和直线b及∠FGC的角平分线GQ的反向延长线交于点N和点M，试说明：∠1+∠2=135°；
（3）如图3，点M为直线a上一点，连结MF，∠MFE的角平分线FN交直线a于点N，过点N作NQ⊥NF交∠HFM的角平分线FQ于点Q，若∠DEA记为β，请直接用含β的代数式来表示∠MNQ+∠HFQ．
组卷：256引用：5难度：0.5
解析