2022-2023学年湖北省部分高中联考协作体高二（上）期中数学试卷

一、选择题（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．若方程（m²-4）x+（m²-2m）y+1=0表示一条直线，则实数m满足（　　）

  A．m≠0

  B．m≠2

  C．m≠±2

  D．m≠±2且m≠0
  组卷：39引用：2难度：0.9

  解析

• 2．已知M，A，B，C为空间中四点，任意三点不共线，且

  OM

  =

  -

  3

  OA

  +

  x

  OB

  +

  y

  OC

  ，若M，A，B，C四点共面，则x+y的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：13引用：2难度：0.7

  解析

• 3．设a、b、c分别是△ABC的对边长，则直线xsinA+ysinB-sinC=0与ax+by-c=0的位置关系是（　　）

  A．平行

  B．垂直

  C．重合

  D．相交
  组卷：5引用：2难度：0.5

  解析

• 4．已知向量{

  a

  ，

  b

  ，

  c

  }是空间的一基底，向量{

  a

  +

  b

  ，

  a

  -

  b

  ，

  c

  }是空间的另一基底，一向量

  p

  在基底{

  a

  ，

  b

  ，

  c

  }下的坐标为（1，2，3），则向量p在基底{

  a

  +

  b

  ，

  a

  -

  b

  ，

  c

  }下的坐标为（　　）

  A．（ 1 2 ， 3 2 ，3）

  B．（ 3 2 ，- 1 2 ，3）

  C．（3，- 1 2 ， 3 2 ）

  D．（- 1 2 ， 3 2 ，3）
  组卷：105引用：8难度：0.5

  解析

• 5．已知圆C：（x-3）²+（y-4）²=1和两点A（-m,0），B（m,0），（m＞0）．若圆C上存在点P，使得∠APB=90°，则m的最小值和最大值分别为（　　）

  A．4，7

  B．4，6

  C．5，7

  D．5，6
  组卷：83引用：2难度：0.5

  解析

• 6．在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上、下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，它的高为4，AA₁，BB₁，CC₁，DD₁均与曲池的底面垂直，底面扇环对应的两个圆的半径分别为2和4，对应的圆心角为90°，则图中异面直线AB₁与CD₁所成角的余弦值为（　　）

  A． 4 5

  B． 3 5

  C． 2 3

  D． 3 4
  组卷：24引用：6难度：0.6

  解析

• 7．已知圆C₁：x²+y²=2，圆C₂：（x-3）²+y²=4．若过点（0，-2）的直线l与圆C₁、C₂都有公共点，则直线斜率的取值范围是（　　）

  A．[-1， 12 5 ]

  B．[0， 12 5 ]

  C．[-1，0]∪[1， 12 5 ]

  D．[1， 12 5 ]
  组卷：9引用：1难度：0.6

  解析

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.除17题为10分外，18～22题均为12分.）

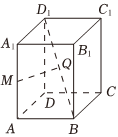• 21．如图，在长方体ABCD-A₁B₁C₁D₁中，AB=3，AD=2，AA₁=4．
  （1）求BD₁与面AA₁C₁C所成角的正弦值；
  （2）如M在AA₁上，Q在BD₁上，当MQ⊥AA₁，MQ⊥BD₁时，求MQ的长度．
  组卷：9引用：2难度：0.5

  解析

• 22．已知圆C经过P（2，0），

  Q

  （

  1

  ，

  3

  ）

  两点，圆心在直线x-y=0上．
  （1）求圆C的标准方程；
  （2）若圆C与y轴相交于A，B两点（A在B上方）．直线l：y=kx+1与圆C交于M，N两点，直线AM，BN相交于点T．请问点T是否在定直线上？若是，求出该直线方程；若不是，说明理由．
  组卷：25引用：2难度：0.7

  解析