2022-2023学年河北省保定市雄县七年级（下）期末数学试卷

一、选择题（本大题有14个小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的)

• 1．下列各数中是无理数的是（　　）

  A．3.1415926

  B． 4

  C． 3 9

  D． 3 8
  组卷：8引用：1难度：0.8

  解析

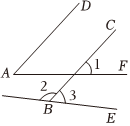• 2．如图，由AD∥BC，可以得到（　　）

  A．∠3=∠A

  B．∠2=∠A

  C．∠1=∠3

  D．∠1=∠A
  组卷：21引用：1难度：0.5

  解析

• 3．若点（-2，a）向下平移3个单位长度后正好落在x轴上，则a的值是（　　）

  A．-2

  B．2

  C．-3

  D．3
  组卷：104引用：1难度：0.8

  解析

• 4．解以下两个方程组：①

  x = 3 y - 5

  2 x - 4 y = 2

  ，②

  2 x + 3 y = 5

  5 x - 3 y = 9

  时，较为简便的方法是（　　）

  A．①用代入法、②用加减法	B．①用加减法、②用代入法
  C．都用代入法	D．都用加减法
  组卷：94引用：1难度：0.5

  解析

• 5．已知m＜n,则下列不等式错误的是（　　）

  A．m+3＜n+3

  B．3m-1＜3n-1

  C． 1 3 m ＜ 1 3 n

  D．-2m＜-2n
  组卷：18引用：1难度：0.7

  解析

• 6．要调查下列问题，需要进行全面调查的是（　　）

  A．调查市场上某种食品的色素含量是否符合国家标准

  B．调查某品牌电池的使用寿命

  C．了解神舟十五号载人飞船设备零件的质量情况

  D．了解全市中小学生每周做家务的时间
  组卷：5引用：1难度：0.8

  解析

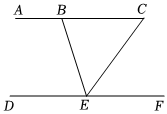• 7．如图，点E在直线DF上，已知∠CEF=52°，∠ABE=108°，若要使得AC∥DF，则∠BEC=（　　）

  A．76°

  B．72°

  C．56°

  D．52°
  组卷：31引用：1难度：0.6

  解析

• 8．已知（x-1）²=4，则x的值是（　　）

  A．3

  B．-3

  C．-1

  D．-1或3
  组卷：105引用：3难度：0.9

  解析

三、解答题（本大题有7个小题，共65分．解答应写出文字说明、证明过程或演算步骤）

• 24．为进一步落实“双减”，增进“双增”，友谊中学要购买若干个足球和篮球，已知购买2个足球和1个篮球共需110元；购买1个足球和2个篮球共需145元．
  （1）求1个足球和1个篮球的价格各是多少元；
  （2）学校准备购买篮球和足球共20个，每种球都要买，且购买金额不能超过600元，请你帮该学校设计购买方案；
  （3）在（2）的前提下，若要求购买的费用最少，请你选择一种最佳的购买方案，并通过计算说明理由．
  组卷：47引用：2难度：0.5

  解析

• 25．已知AB∥CD，直线EF和直线AB，CD分别交于点A，C，并把平面分成六个区域（如图甲），点P是六个区域中（不在直线AB，CD，EF上）的任意一点，连接PA，PC．
  （1）图乙是点P在区域⑤的情况，嘉嘉猜想出∠APC，∠A，∠C之间的数量关系，请帮她完善证明过程；
  嘉嘉猜想的结论是：∠APC=∠A+∠C．
  证明：过点P作PQ∥AB，
  ∴∠1=∠

  （

  ）．
  ∵AB∥CD，PQ∥AB，
  ∴CD∥PQ （

  ）．
  ∴∠2=∠

  （

  ）．
  ∴∠1+∠2=

  ．
  又∠1+∠2=∠APC，
  ∴∠APC=∠A+∠C．
  （2）图丙是点P在区域②的情况，那么（1）中的结论还成立吗？请加以证明；
  （3）请你探索点P在①③④⑥区域时的情况，并直接写出∠APC，∠A，∠C之间的数量关系．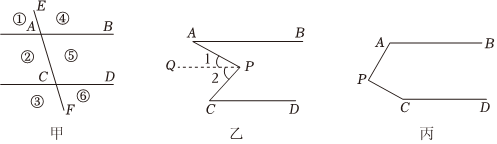
  
  组卷：83引用：1难度：0.5

  解析