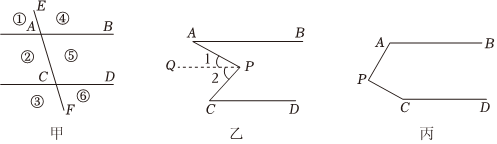
已知AB∥CD，直线EF和直线AB，CD分别交于点A，C，并把平面分成六个区域（如图甲），点P是六个区域中（不在直线AB，CD，EF上）的任意一点，连接PA，PC．
（1）图乙是点P在区域⑤的情况，嘉嘉猜想出∠APC，∠A，∠C之间的数量关系，请帮她完善证明过程；
嘉嘉猜想的结论是：∠APC=∠A+∠C．
证明：过点P作PQ∥AB，
∴∠1=∠BAPBAP（ 两直线平行，内错角相等两直线平行，内错角相等）．
∵AB∥CD，PQ∥AB，
∴CD∥PQ （ 如果两条直线都与第三条直线平行，那么这两条直线也互相平行如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．
∴∠2=∠DCPDCP（ 两直线平行，内错角相等两直线平行，内错角相等）．
∴∠1+∠2=∠BAP+∠DCP∠BAP+∠DCP．
又∠1+∠2=∠APC，
∴∠APC=∠A+∠C．
（2）图丙是点P在区域②的情况，那么（1）中的结论还成立吗？请加以证明；
（3）请你探索点P在①③④⑥区域时的情况，并直接写出∠APC，∠A，∠C之间的数量关系．
【答案】BAP；两直线平行，内错角相等；如果两条直线都与第三条直线平行，那么这两条直线也互相平行；DCP；两直线平行，内错角相等；∠BAP+∠DCP
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：83引用：1难度：0.5
相似题
-
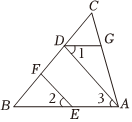1．推理填空：
如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
因为EF∥AD，
所以∠2=．（ ）
又因为∠1=∠2，
所以∠1=∠3．（ ）
所以AB∥．（ ）
所以∠BAC+=180°（ ）
又因为∠BAC=70°，
所以∠AGD=．发布：2025/6/18 7:0:1组卷：1131引用：35难度：0.7 -
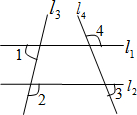2．如图，已知∠1=70°，∠2=110°，∠3=80°，则∠4=．发布：2025/6/18 0:30:4组卷：165引用：6难度：0.7 -
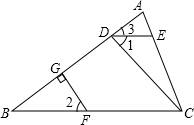3．如图，在△ABC中，∠1=∠2，∠3=∠B，FG⊥AB于G，猜想CD与AB的位置关系，并证明你的猜想．发布：2025/6/18 12:30:1组卷：167引用：5难度：0.7
