当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省宿迁市沭阳县九年级（上）月考数学试卷（9月份）

发布：2024/9/4 6:0:10

一、选择题。（本大题共有8小题，每小题3分，共24分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

1．下列方程中，关于x的一元二次方程的是（　　）
A．x+y=1 B．3x+y²=2 C．2x-x²=3 D．x+
1
x
=4
组卷：65引用：8难度：0.8
解析
2．用配方法解方程x²-4x-4=0时，原方程应变形为（　　）
A．（x-2）²=0 B．（x-2）²=8 C．（x+2）²=0 D．（x+2）²=8
组卷：927引用：21难度：0.8
解析
3．⊙O的半径为3，点A到圆心O的距离为4，点A与⊙O的位置关系是（　　）
A．点A在⊙O外 B．点A在⊙O内 C．点A在⊙O上 D．不能确定
组卷：210引用：10难度：0.9
解析
4．若关于x的一元二次方程x²+3x+4=0，该方程的解的情况是（　　）
A．没有实数根 B．有两个不相等的实数根
C．有两个相等的实数根 D．不能确定
组卷：317引用：8难度：0.6
解析
5．下列结论正确的是（　　）
A．三点确定一个圆
B．相等的圆心角所对的弧相等
C．等弧所对的弦相等
D．三角形的外心到三角形各边的距离相等
组卷：235引用：3难度：0.6
解析
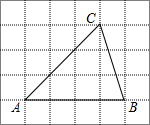6．如图，将△ABC放在每个小正方形边长为1的网格中，点A、B、C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面半径是（　　）
A．
5
B．
6
C．2 D．
5
2
组卷：2841引用：26难度：0.9
解析
7．已知3是关于x的方程x²-（m+1）x+2m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为（　　）
A．7 B．10 C．11 D．10或11
组卷：9559引用：54难度：0.7
解析
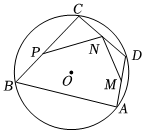8．如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为
ˆ
AC
上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为6，则PN+MN的长度的最大值是（　　）
A．6 B．12 C．
3
+
3
3
D．
6
+
3
3
组卷：498引用：1难度：0.5
解析

二、填空题。（本大题共10小题，每小题3分，共30分，不需要写出解答过程。）

9．一元二次方程x²=x的根
．
组卷：441引用：96难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题。（本题共10小题，共96分。解答时写出必要的文字说明、证明过程或演算步骤）

27．探索一个问题：任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半（完成下列空格）．
（1）当已知矩形A的边长分别是6和1时，小亮同学是这样研究的：设所求矩形的两边分别是x,y,由题意得方程组
x
+
y
=
7
2
xy
=
3
，消去y化简得2x²-7x+6=0：
∵Δ=49-48＞0，x₁=
；x₂=
；所以满足要求的B存在；
（2）如果已知矩形A的边长分别是2和1，请你仿照小亮方法研究是否存在满足要求的矩形B；
（3）如果矩形A的边长为m,n,请你研究满足什么条件时，矩形B存在？
组卷：303引用：7难度：0.6
解析
28．（1）【基础巩固】如图1，△ABC内接于⊙O，若∠C=60°，弦AB=4
3
，则半径r=
；
（2）【问题探究】如图2，四边形ABCD的四个顶点均在⊙O上，若∠ADC=60°，AD=DC，点B为弧AC上一动点（不与点A，点C重合）．求证：AB+BC=BD；
（3）【解决问题】如图3，一块空地由三条直路（线段AD、AB、BC）和一条道路劣弧
ˆ
CD
围成，已知CM=DM=
3
千米，∠DMC=60°，
ˆ
CD
的半径为1千米，市政府准备将这块空地规划为一个公园，主入口在点M处，另外三个入口分别在点C、D、P处，其中点P在
ˆ
CD
上，并在公园中修四条慢跑道，即图中的线段DM、MC、CP、PD，某数学兴趣小组探究后发现C、P、D、M四个点在同一个圆上，请你帮他们证明C、P、D、M四点共圆，并判断是否存在一种规划方案，使得四条慢跑道总长度（即四边形DMCP的周长）最大？若存在，求其最大值；若不存在，说明理由．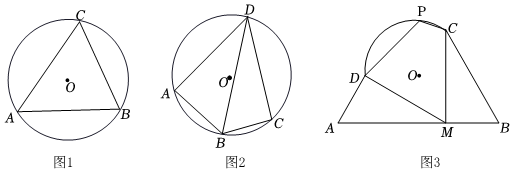

组卷：311引用：5难度：0.1
解析