2023-2024学年重庆市两江育才中学高二（上）质检数学试卷

一、单选题（本大题共8小题，共40分.在每小题列出的选项中，选出符合题目的一项）

• 1．设x,y∈R，向量

  a

  =（x,1，1），

  b

  =（1，y,1），

  c

  =（2，-4，2），且

  a

  ⊥

  c

  ，

  b

  ∥

  c

  ，则|

  a

  +

  b

  |=（　　）

  A． 2 2

  B． 10

  C．3

  D．4
  组卷：2698引用：74难度：0.8

  解析

• 2．若A（6，-1，4），B（1，-2，1），C（4，2，3），则△ABC的形状是（　　）

  A．不等边锐角三角形	B．直角三角形
  C．钝角三角形	D．等边三角形
  组卷：101引用：5难度：0.9

  解析

• 3．已知圆锥的底面半径为4，其侧面展开图是一个圆心角为

  8

  π

  5

  的扇形，则该圆锥的体积为（　　）

  A．48π

  B．45π

  C．16π

  D．15π
  组卷：434引用：7难度：0.8

  解析

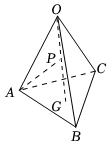• 4．如图，在四面体OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，G为△ABC的重心，P为OG的中点，则

  AP

  =（　　）

  A． - 2 3 a + 1 3 b + 1 3 c	B． 1 6 a - 1 3 b - 1 3 c
  C． - 5 6 a + 1 6 b + 1 6 c	D． 5 6 a - 1 3 b - 1 3 c
  组卷：810引用：11难度：0.8

  解析

• 5．在△ABC中，角A，B，C的对边分别为a,b,c,b²-c²=2a²，c=2a,则cosB=（　　）

  A． - 1 2

  B． - 1 4

  C． 1 2

  D． 3 2
  组卷：264引用：4难度：0.7

  解析

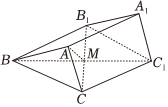• 6．如图，在三棱柱ABC-A₁B₁C₁中，AB=AC=2，AA₁=3，∠BAC=60°，∠A₁AC=∠A₁AB=120°，B₁C与BC₁的交点为M，则AM=（　　）

  A． 1 2

  B． 5 4

  C． 3 2

  D． 10 4
  组卷：55引用：6难度：0.7

  解析

• 7．在正三棱柱ABC-A₁B₁C₁中，

  AB

  =

  3

  ，点D在棱BC上运动，若AD+DB₁的最小值为

  13

  ，则三棱柱ABC-A₁B₁C₁的外接球的表面积为（　　）

  A．8π

  B．16π

  C．20π

  D．32π
  组卷：152引用：10难度：0.5

  解析

四、解答题.

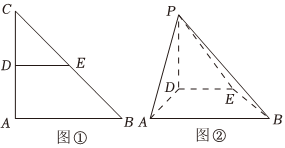• 21．如图①，在等腰直角三角形ABC中，∠A=90°，AB=3．D、E分别是AC、BC上的点，且满足DE∥AB．将△CDE沿DE折起，得到如图②所示的四棱锥P-ABED．
  （1）设平面ABP∩平面DEP=l,证明：l⊥面ADP；
  （2）若PA=

  5

  ，DE=2．求直线PD与平面PEB所成角的正弦值．
  组卷：127引用：5难度：0.5

  解析

• 22．如图，在三棱台ABC-A₁B₁C₁中，若A₁A⊥平面ABC，AB⊥AC，AB=AC=AA₁=2，A₁C₁=1，N为AB中点，M为棱BC上一动点（不包含端点）．
  （1）若M为BC的中点，求证：A₁N∥平面C₁MA；
  （2）是否存在点M，使得平面C₁MA与平面ACC₁A₁所成角的余弦值为

  6

  6

  ？若存在，求出BM长度；若不存在，请说明理由．
  组卷：538引用：12难度：0.5

  解析