当前位置：试卷中心 > 试卷详情

2019-2020学年浙江省台州市临海市八年级（上）期末数学试卷

发布：2024/9/12 4:0:8

一、选择题（本大题共10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）.

1．下列手机APP图案中，属于轴对称图形的是（　　）
A． B． C． D．
组卷：14引用：1难度：0.7
解析
2．现要用三根木棒搭一个三角形．已知其中两根木棒的长分别是2cm和5cm,那么第三根的长可以是（　　）
A．1cm B．3cm C．5cm D．7cm
组卷：16引用：1难度：0.7
解析
3．如图，人字梯中间一般都会设计一根拉杆，这样做的几何原理是（　　）
A．两直线平行，同位角相等
B．等边对等角
C．两点之间，线段最短
D．三角形的稳定性
组卷：38引用：3难度：0.6
解析
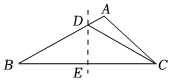4．如图，DE是△ABC边上的垂直平分线，∠A=110°，∠B=30°，则∠ACD的度数是（　　）
A．10° B．13° C．15° D．18°
组卷：41引用：2难度：0.7
解析
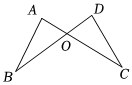5．如图，线段AC与BD交于点O．现有四个条件：①OA=OD；②OB=OC；③AB=DC；④∠A=∠D．下列选项中不能判定△AOB≌△DOC的是（　　）
A．①② B．①④ C．②③ D．③④
组卷：29引用：2难度：0.6
解析
6．下列计算结果为x⁷的是（　　）
A．x¹⁴÷x² B．x¹⁴÷x⁷ C．（x²）⁵ D．x³+x⁴
组卷：24引用：1难度：0.7
解析
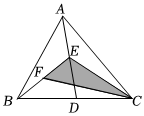7．如图，在△ABC中，点D，E，F分别是BC，AD，BE的中点，若△CEF的面积为1，则△ABC的面积为（　　）
A．2 B．3 C．4 D．5
组卷：118引用：2难度：0.7
解析
8．甲，乙两名学生参加校运会200米跑步比赛．甲在前半段的速度是每秒a米，后半段的速度是每秒b米（a＞b），共用时t₁秒；乙以每秒
a
+
b
2
米的速度跑完全程，共用时t₂秒．则t₁和t₂的大小关系为（　　）
A．t₁＞t₂ B．t₁=t₂ C．t₁＜t₂ D．无法确定
组卷：37引用：1难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共6小题，第21～23题每题6分，第24题8分，第25题12分，第26题12分，共50分）．

25．阅读材料：我们知道，对一个图形通过两种不同的方法计算它的面积，可以得到一个数学等式．如图①，将一个边长为a的正方形纸片减去一个边长为b的小正方形，根据剩下部分的面积，可以得到等式：a²-b²=a（a-b）+b（a-b），将等式右边因式分解，即a²-b²=（a-b）（a+b）．

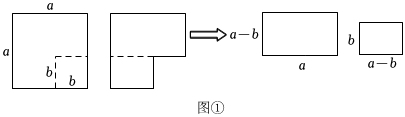
请类比上述探究过程，解答下列问题：
（1）如图②，将一个棱长为a的正方体木块挖去一个棱长为b的小正方体，根据剩下部分的体积，可以得到等式：
，将等式右边因式分解，即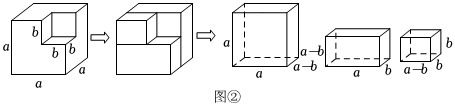
；

（2）类比以上探究过程，可得a³+b³=（
）（
）；
（3）根据以上探究的结果：
①计算：
（
2019
+
1
）
3
-
（
2019
-
1
）
3
；
②将y⁶-1因式分解成四个整式乘积的形式：
y⁶-1=（
）（
）（
）（
）．
组卷：140引用：1难度：0.5
解析
26．定义：连接三角形两边中点的线段叫做三角形的中位线．
性质：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
理解：如图①，在△ABC中，点D，E分别是AB，AC的中点，那么DE为△ABC的一条中位线．可得DE∥BC且DE=
1
2
BC．
应用：如图②，在△ABC中，AB=AC，点D，E分别在边AB，AC上，且AD=AE．点M，N，P分别是DE，BC和CD的中点．已知∠BAC=α．
（1）当α=90°时，
①请直接写出：PM与PN的数量关系
；∠MPN=
．
②是否存在点D，使得以P，M，N为顶点的三角形与△ADE全等？若存在，请求出点D的位置；若不存在，请说明理由．
（2）将△ADE绕点A旋转，当点D在△ABC内时（如图③），
①试说明PM与PN的数量关系，并求出∠MPN的度数（用含α的式子表示）；
②连接BD，MN，若AD=BD，直接写出△ADE和△PMN的面积关系：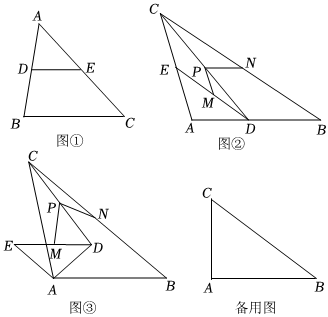
．
组卷：165引用：1难度：0.1
解析