2022-2023学年湖北省武汉市华中师大一附中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.（在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．已知i为虚数单位，则（cos75°+isin75°）（cos15°+isin15°）=（　　）

  A．-1

  B．1

  C．-i

  D．i
  组卷：55引用：2难度：0.7

  解析

• 2．如果一组数据的中位数比平均数小很多，则下列叙述一定错误的是（　　）

  A．数据中可能有异常值

  B．这组数据是近似对称的

  C．数据中可能有极端大的值

  D．数据中众数可能和中位数相同
  组卷：102引用：4难度：0.7

  解析

• 3．有2个人在一座8层大楼的底层进入电梯，假设每一个人从第二层开始在每一层离开电梯是等可能的，则这两人在不同层离开电梯的概率为（　　）

  A． 3 7

  B． 6 7

  C． 7 8

  D． 7 16
  组卷：58引用：2难度：0.7

  解析

• 4．已知点A的坐标为

  （

  1

  ，

  3

  ）

  ，将

  OA

  绕坐标原点O逆时针旋转90°，得到

  OB

  ，则点B的横坐标为（　　）

  A． - 3

  B．-1

  C． 3

  D．1
  组卷：35引用：2难度：0.7

  解析

• 5．某调查机构抽取了部分关注济南地铁建设的市民作为样本，分析其年龄和性别结构，并制作出如下等高条形图．根据图中（35岁以上含35岁）的信息，关于该样本的结论不一定正确的是（　　）
  

  A．男性比女性更关注地铁建设

  B．关注地铁建设的女性多数是35岁以上

  C．35岁以下的男性人数比35岁以上的女性人数多

  D．35岁以上的人对地铁建设关注度更高
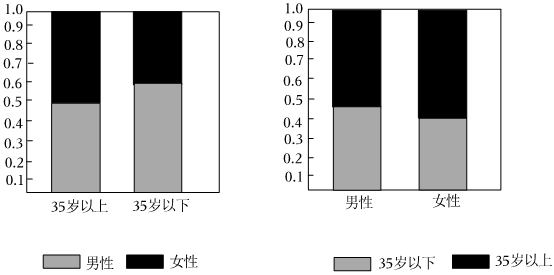  组卷：108引用：4难度：0.7

  解析

• 6．已知l,m,n是三条不同的直线，α，β，γ是三个不同的平面，给出下列命题，其中真命题是（　　）

  A．若l⊥α，l⊥m,则m∥α

  B．若α∩β=l,β∩γ=m,γ∩α=n,l∥m,则m∥n

  C．若α⊥β，l⊂α，m⊂β，则l⊥m

  D．l⊂α，l⊥m,l⊥n,m∥β，n∥β，则α∥β
  组卷：181引用：3难度：0.6

  解析

• 7．设平面向量

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  b

  在

  a

  方向上的投影向量为

  c

  ，则（　　）

  A． a • c = c • b

  B． a • b = a • c

  C．| a • c |≤2

  D． a • c = | a | • | c |
  组卷：91引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异，经过大量调查，得到如图的患病者和未患病者该指标的频率分布直方图：
  
  利用该指标制定一个检测标准，需要确定临界值c,将该指标大于c的人判定为阳性，小于或等于c的人判定为阴性．此检测标准的漏诊率是将患病者判定为阴性的概率，记为p（c）；误诊率是将未患病者判定为阳性的概率，记为q（c）．假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率．
  （1）当漏诊率p（c）=0.5%时，求临界值c和误诊率q（c）；
  （2）设函数f（c）=p（c）+q（c），当c∈[95，105]时，求f（c）的解析式，并求f（c）在区间[95，105]的最小值．
  
  组卷：212引用：9难度：0.7

  解析

• 22．如图，四棱台ABCD-A₁B₁C₁D₁中，上、下底面均是正方形，且侧面是全等的等腰梯形，AB=2A₁B₁=4，E、F分别为DC、BC的中点，上下底面中心的连线O₁O垂直于上下底面，且O₁O与侧棱所在直线所成的角为45°．
  （1）求证：BD₁∥平面C₁EF；
  （2）线段BF上是否存在点M，使得直线A₁M与平面C₁EF所成的角的正弦值为

  3

  22

  22

  ，若存在，求出线段BM的长；若不存在，请说明理由．
  组卷：159引用：5难度：0.5

  解析