当前位置：试卷中心 > 试卷详情

2023-2024学年河南省周口恒大中学高二（上）月考数学试卷（10月份）

发布：2024/9/23 6:0:8

1．在两坐标轴上的截距相等，且与圆（x-3）²+（y-4）²=2相切的直线有（　　）条
A．1 B．2 C．3 D．4
组卷：44引用：3难度：0.8
解析
2．若圆
C
1
：
x
2
+
y
2
=
1
与圆
C
2
：
（
x
-
a
）
2
+
（
y
-
b
）
2
=
1
的公共弦AB的长为1，则直线AB的方程为（　　）
A．2ax+by-1=0 B．2ax+by-3=0
C．2ax+2by-1=0 D．2ax+2by-3=0
组卷：208引用：4难度：0.6
解析
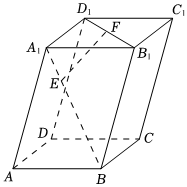3．如图，在平行六面体ABCD-A₁B₁C₁D₁中，点E在面对角线A₁B上，满足
A
1
E
=
1
3
A
1
B
，点F为面对角线B₁D₁的中点，若
A
A
1
=
a
，
AB
=
b
，
AD
=
c
，则
EF
=（　　）
A．
1
3
a
+
1
6
b
+
1
2
c
B．
1
6
a
+
1
3
b
+
1
2
c
C．
1
2
a
+
1
3
b
+
1
6
c
D．
1
6
a
+
1
2
b
+
1
3
c
组卷：74引用：5难度：0.8
解析
4．设点P是曲线f（x）=x-2lnx上任意一点，则P到直线x+y+2=0的距离的最小值为（　　）
A．
2
B．2 C．
2
2
D．
3
2
-
2
ln
2
组卷：338引用：5难度：0.5
解析
5．已知m≠0，直线ax+3my+2a=0在两坐标轴上的截距之和为2，则直线的斜率为（　　）
A．1 B．
-
1
3
C．
-
2
3
D．2
组卷：33引用：1难度：0.8
解析
6．若直线l：ax+by+1=0平分圆C：x²+y²+2x+2y-1=0的周长，则a+b=（　　）
A．1 B．2 C．-1 D．-2
组卷：36引用：1难度：0.7
解析
7．若直线
y
=
2
x
与圆（x-a）²+y²=2（a＞0）相切，则a=（　　）
A．
3
B．2 C．3 D．
2
3
组卷：134引用：4难度：0.7
解析

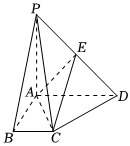21．已知四棱锥P-ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AB=AD=2BC=2，E为PD中点．
（1）求证：CE∥平面PAB；
（2）设平面EAC与平面DAC的夹角为45°，求三棱锥E-ACD的体积．
组卷：44引用：4难度：0.4
解析
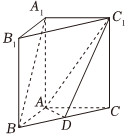22．已知在三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，AB⊥AC，且AB=AC=1，
A
A
1
=
3
，点D是BC的中点．
（1）求证：A₁B∥平面AC₁D；
（2）在棱CC₁上是否存在一点M，使B₁M⊥平面AC₁D？若存在，指出点M的位置并证明，若不存在，说明理由．
组卷：83引用：2难度：0.5
解析

A． 1 3 a + 1 6 b + 1 2 c	B． 1 6 a + 1 3 b + 1 2 c
C． 1 2 a + 1 3 b + 1 6 c	D． 1 6 a + 1 2 b + 1 3 c

A．2ax+by-1=0	B．2ax+by-3=0
C．2ax+2by-1=0	D．2ax+2by-3=0

1．在两坐标轴上的截距相等，且与圆（x-3）2+（y-4）2=2相切的直线有（ ）条