2022-2023学年江苏省南通市市区八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

• 1．下列志愿服务标志为中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：124引用：3难度：0.9

  解析

• 2．下列事件为随机事件的是（　　）

  A．通常加热到100℃时水沸腾

  B．三角形的内角和是360°

  C．掷骰子一次向上点数不小于1

  D．经过有信号灯的路口时遇到红灯
  组卷：77引用：1难度：0.7

  解析

• 3．函数y=

  x

  -

  3

  中自变量x的取值范围是（　　）

  A．x＞3

  B．x≠3

  C．x≥3

  D．x≥0
  组卷：576引用：10难度：0.9

  解析

• 4．甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩均是9.2环．方差分别为0.42，0.56，0.78，0.63，四人中成绩最稳定的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：91引用：2难度：0.7

  解析

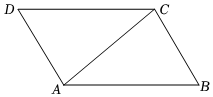• 5．在▱ABCD中（如图），连接AC，已知∠BAC=40°，∠ACB=80°，则∠BCD=（　　）

  A．80°

  B．100°

  C．120°

  D．140°
  组卷：1207引用：19难度：0.6

  解析

• 6．关于x的一元二次方程x²+4x+m=0有两个不相等的实数根，则m的值可能是（　　）

  A．9

  B．6

  C．4

  D．-1
  组卷：413引用：8难度：0.6

  解析

• 7．为了解某小区居民的用水情况，随机抽查了若干户家庭的某月用水量，统计结果如图．这若干户家庭该月用水量的众数是（　　）

  月用水量（吨）	3		4			5			6
  户数	4		6			8			2

  A．5

  B．6

  C．6.5

  D．8
  组卷：62引用：2难度：0.7

  解析

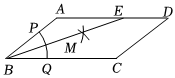• 8．如图，在▱ABCD中，AB=3，BC=5，以点B为圆心，任意长为半径作弧，分别交BA，BC于点P，Q，再分别以P，Q为圆心，大于

  1

  2

  PQ

  长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：192引用：4难度：0.4

  解析

三、解答题（本大题共8小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

• 25．如图1，在矩形ABCD中，AB=6cm,

  AD

  =

  3

  2

  cm,点E，F分别从点B，A出发，同时以每秒1cm的速度沿直线AB向左运动，当点E与点A重合时两点都停止运动，设运动时间为t秒．连接DF，CE，得到四边形CEFD．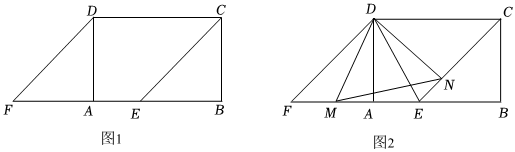
  
  （1）当运动时间t为多少秒时，四边形CEFD是菱形？
  （2）如图2，在（1）的条件下，连接DE．将∠FDE绕点D逆时针旋转，在旋转过程中∠FDE的两边与线段FE，EC分别交于点M，N，连接MN．
  ①当DN⊥CE时，旋转角∠FDM的度数为

  度，FM的长度为

  cm；
  ②试探究线段MF，CN，MN之间的数量关系，并说明理由．
  组卷：330引用：1难度：0.3

  解析

• 26．定义：函数图象上到两坐标轴的距离都不大于n（n≥0）的点叫做这个函数图象的“n级限距点”．例如，点（

  1

  3

  ，

  1

  3

  ）是函数y=x图象的“

  1

  3

  级限距点”；点（2，1）是函数y=-

  1

  2

  x+2图象的“2级限距点”．
  （1）在①（-

  1

  2

  ，-1）；②（-

  1

  3

  ，-

  2

  3

  ）；③（1，2）三点中，是函数y=2x图象的“1级限距点”的有

  （填序号）；
  （2）若y关于x的一次函数y=kx+3图象的“2级限距点”有且只有一个，求k的值；
  （3）若y关于x的函数y=-|x-

  n

  2

  |-2n+1图象存在“n级限距点”，求出n的取值范围．
  组卷：460引用：1难度：0.4

  解析