当前位置：试卷中心 > 试卷详情

2023-2024学年广东省佛山市顺德一中南校区高二（上）第一次月考数学试卷

发布：2024/8/29 12:0:8

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1．已知复数z=
3
+
i
1
+
i
（i是虚数单位），则
z
所对应的点所在象限为（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：44引用：6难度：0.7
解析
2．已知一个古典概型的样本空间Ω和事件A和B，其中n（Ω）=12，n（A）=6，n（B）=4，n（A∪B）=8，那么下列事件概率错误的是（　　）
A．
P
（
AB
）
=
1
6
B．
P
（
A
∪
B
）
=
2
3
C．
P
（
A
B
）
=
1
6
D．
P
（
A
B
）
=
2
3
组卷：382引用：3难度：0.8
解析
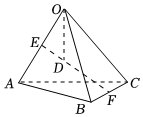3．如图，E，F分别是四面体OABC的棱OA、BC的中点，D是线段EF的一个四等分点（靠近E点），设
OA
=
a
，
OB
=
b
，
OC
=
c
，则
OD
=（　　）
A．
1
6
a
+
1
3
b
+
1
3
c
B．
1
3
a
+
1
6
b
+
1
3
c
C．
3
8
a
+
1
8
b
+
1
8
c
D．
1
6
a
+
1
3
b
+
1
6
c
组卷：68引用：2难度：0.8
解析
4．已知向量
a
=
（
1
，
3
，
0
）
，
b
=
（
2
，
1
，
1
）
，则向量
a
在向量
b
上的投影向量
c
=（　　）
A．
（
5
2
，
5
4
，
5
4
）
B．
（
5
3
，
5
6
，
5
6
）
C．
（
5
4
，
5
8
，
5
8
）
D．（2，4，4）
组卷：933引用：5难度：0.8
解析
5．将一骰子抛掷两次，所得向上点数分别为m和n,则函数y=mx²-4nx+1在[1，+∞）上是增函数的概率是（　　）
A．
1
6
B．
1
4
C．
3
4
D．
5
6
组卷：209引用：4难度：0.5
解析
6．在△ABC中，内角A，B，C所对的边分别为a,b,c.若A=45°，b=2
2
，且△ABC的面积是1，则△ABC的外接圆的面积为（　　）
A．
5
π B．
5
2
π
C．
10
2
π
D．4π
组卷：124引用：6难度：0.7
解析
7．已知圆锥的顶点为S，母线SA，SB所成角的余弦值为
7
8
，SA与圆锥底面所成角为45°，若△SAB的面积为5
15
，则该圆锥的侧面积为（　　）
A．40
2
π B．80
2
C．40
3
π D．80
3
π
组卷：463引用：10难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

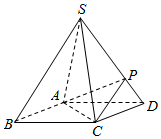21．如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的
2
倍，P为侧棱SD上的点．
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求平面PAC与平面ACD的夹角大小；
（3）在（2）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC？若存在，求SE：EC的值；若不存在，试说明理由．
组卷：230引用：3难度：0.5
解析
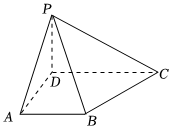22．如图，四棱锥P-ABCD中，底面ABCD为梯形，PD⊥底面ABCD，AB∥CD，AD⊥CD，AD=AB=1，BC=
2
．过A作一个平面α使得α∥平面PBC．
（1）求平面α将四棱锥P-ABCD分成两部分几何体的体积之比．
（2）若平面α与平面PBC之间的距离为
6
6
，求直线PA与平面PBC所成角的正弦值．
组卷：44引用：2难度：0.5
解析